如图,已知 ,在射线 上取点 ,以 为圆心的圆与 相切;在射线 上取点 ,以 为圆心, 为半径的圆与 相切;在射线 上取点 ,以 为圆心, 为半径的圆与 相切; ;在射线 上取点 ,以 为圆心, 为半径的圆与 相切.若 的半径为1,则 的半径长是 .

下列图形都是由同样大小的菱形按照一定规律组成的,其中第①个图形中共有3个菱形,第②个图形中共有7个菱形,第③个图形中共有13个菱形……按此规律排列下去,第 个图形中菱形的个数为10101个.

设 的面积为1.
如图1,分别将 , 边2等分, , 是其分点,连接 , 交于点 ,得到四边形 ,其面积 .
如图2,分别将 , 边3等分, , , , 是其分点,连接 , 交于点 ,得到四边形 ,其面积 ;
如图3,分别将 , 边4等分, , , , , , 是其分点,连接 , 交于点 ,得到四边形 ,其面积 ;
按照这个规律进行下去,若分别将 , 边 等分, ,得到四边形 ,其面积 .

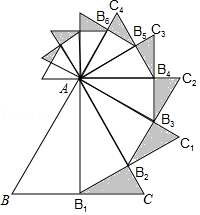
如图,已知等边 的边长是2,以 边上的高 为边作等边三角形,得到第一个等边△ ;再以等边△ 的 边上的高 为边作等边三角形,得到第二个等边△ ;再以等边△ 的 边上的高 为边作等边三角形,得到第三个等边△ ; ,记△ 的面积为 ,△ 的面积为 ,△ 的面积为 ,如此下去,则 或 .
如图, 第一个图形中有 1 个点, 第二个图形中有 4 个点, 第三个图形中有 13 个点, ,按此规律, 第 个图形中有 个点 .

将一些相同的“○”按如图所示的规律依次摆放,观察每个“龟图”中的“○”的个数,若第n个“龟图”中有245个“○”,则n= .

某广场用同一种如图所示的地砖拼图案,第一次拼成形如图1所示的图案,第二次拼成形如图2所示的图案,第三次拼成形如图3所示的图案,第四次拼成形如图4所示的图案 按照这样的规律进行下去,第 次拼成的图案共用地砖 块.

如图,∠MON=60°,作边长为1的正六边形A1B1C1D1E1F1,边A1B1、F1E1分别在射线OM、ON上,边C1D1所在的直线分别交OM、ON于点A2、F2,以A2F2为边作正六边形A2B2C2D2E2F2,边C2D2所在的直线分别交OM、ON于点A3、F3,再以A3F3为边作正六边形A3B3C3D3E3F3,…,依此规律,经第n次作图后,点Bn到ON的距离是 .

如图,用大小相同的小正方形拼大正方形,拼第1个正方形需要4个小正方形,拼第2个正方形需要9个小正方形 ,按这样的方法拼成的第 个正方形比第 个正方形多 个小正方形.

如图,把 个边长为1的正方形拼接成一排,求得 , , ,计算 , 按此规律,写出 (用含 的代数式表示).

试题篮
()