经过一年多的精准帮扶,小明家的网络商店(简称网店)将红枣、小米等优质土特产迅速销往全国.小明家网店中红枣和小米这两种商品的相关信息如下表:
商品 |
红枣 |
小米 |
规格 |
|
|
成本(元 |
40 |
38 |
售价(元 |
60 |
54 |
根据上表提供的信息,解答下列问题:
(1)已知今年前五个月,小明家网店销售上表中规格的红枣和小米共,获得利润4.2万元,求这前五个月小明家网店销售这种规格的红枣多少袋;
(2)根据之前的销售情况,估计今年6月到10月这后五个月,小明家网店还能销售上表中规格的红枣和小米共,其中,这种规格的红枣的销售量不低于
.假设这后五个月,销售这种规格的红枣为
,销售这种规格的红枣和小米获得的总利润为
(元
,求出
与
之间的函数关系式,并求这后五个月,小明家网店销售这种规格的红枣和小米至少获得总利润多少元.
某樱桃种植户有20吨樱桃待售,现有两种销售方式:一是批发,二是零售.经过市场调查,这两种销售方式对这个种植户而言,每天的销量及每吨所获的利润如下表:
销售方式 |
每天销量(吨 |
每吨所获利润(元 |
批发 |
3 |
4000 |
零售 |
1 |
6000 |
假设该种植户售完20吨樱桃,共批发了吨,所获总利润为
元.
(1)求出与
之间的函数关系式;
(2)若受客观因素影响,这个种植户每天只能采用一种销售方式销售,且正好10天销售完所有樱桃,请计算该种植户所获总利润是多少元?
某校为改善办学条件,计划购进、
两种规格的书架,经市场调查发现有线下和线上两种购买方式,具体情况如下表:
规格 |
线下 |
线上 |
|||
单价(元 |
运费(元 |
单价(元 |
运费(元 |
||
240 |
0 |
210 |
20 |
||
300 |
0 |
250 |
30 |
||
(1)如果在线下购买、
两种书架20个,共花费5520元,求
、
两种书架各购买了多少个
(2)如果在线上购买、
两种书架20个,共花费
元,设其中
种书架购买
个,求
关于
的函数关系式.
(3)在(2)的条件下,若购买种书架的数量不少于
种书架的2倍,请求出花费最少的购买方案,并计算按照这种购买方案线上比线下节约多少钱.
为奖励在社会实践活动中表现优异的同学,某校准备购买一批文具袋和水性笔作为奖品.已知文具袋的单价是水性笔单价的5倍,购买5支水性笔和3个文具袋共需60元.
(1)求文具袋和水性笔的单价;
(2)学校准备购买文具袋10个,水性笔若干支(超过10支).文具店给出两种优惠方案:
:购买一个文具袋,赠送1支水性笔
:购买水性笔10支以上,超出10支的部分按原价的八折优惠,文具袋不打折
①设购买水性笔 支,选择方案 的总费用为 元,选择方案 的总费用为 元,分别求出 , 与 的函数关系式;
②该学校选择哪种方案更合算?请说明理由.
学校准备添置一批课桌椅,原计划订购60套,每套100元,店方表示:如果多购,可以优惠.结果校方实际订购了72套,每套减价3元,但商店获得了同样多的利润.
(1)求每套课桌椅的成本;
(2)求商店获得的利润.
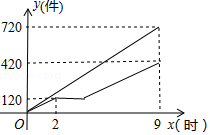
甲、乙两车间同时开始加工一批服装.从开始加工到加工完这批服装甲车间工作了9小时,乙车间在中途停工一段时间维修设备,然后按停工前的工作效率继续加工,直到与甲车间同时完成这批服装的加工任务为止.设甲、乙两车间各自加工服装的数量为(件
.甲车间加工的时间为
(时
,
与
之间的函数图象如图所示.
(1)甲车间每小时加工服装件数为 件;这批服装的总件数为 件.
(2)求乙车间维修设备后,乙车间加工服装数量与
之间的函数关系式;
(3)求甲、乙两车间共同加工完1000件服装时甲车间所用的时间.
为实施乡村振兴战略,解决某山区老百姓出行难的问题,当地政府决定修建一条高速公路.其中一段长为146米的山体隧道贯穿工程由甲乙两个工程队负责施工.甲工程队独立工作2天后,乙工程队加入,两工程队又联合工作了1天,这3天共掘进26米.已知甲工程队每天比乙工程队多掘进2米,按此速度完成这项隧道贯穿工程,甲乙两个工程队还需联合工作多少天?
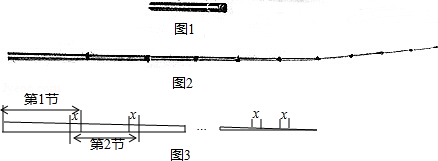
如图是一根可伸缩的鱼竿,鱼竿是用10节大小不同的空心套管连接而成.闲置时鱼竿可收缩,完全收缩后,鱼竿长度即为第1节套管的长度(如图1所示):使用时,可将鱼竿的每一节套管都完全拉伸(如图2所示).图3是这跟鱼竿所有套管都处于完全拉伸状态下的平面示意图.已知第1节套管长 ,第2节套管长 ,以此类推,每一节套管均比前一节套管少 .完全拉伸时,为了使相邻两节套管连接并固定,每相邻两节套管间均有相同长度的重叠,设其长度为 .
(1)请直接写出第5节套管的长度;
(2)当这根鱼竿完全拉伸时,其长度为 ,求 的值.
《九章算术》中有一道阐述“盈不足术”的问题,原文如下:
今有人共买物,人出八,盈三;人出七,不足四.问人数,物价各几何?
译文为:
现有一些人共同买一个物品,每人出8元,还盈余3元;每人出7元,则还差4元,问共有多少人?这个物品的价格是多少?
请解答上述问题.
已知数轴上有A、B、C三点,分别代表﹣24,﹣10,10,两只电子蚂蚁甲、乙分别从A、C两点同时相向而行,甲的速度为4个单位/秒,乙的速度为6个单位/秒.
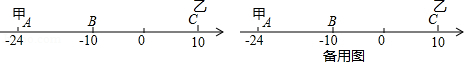
(1)甲、乙多少秒后相遇?
(2)甲出发多少秒后,甲到A、B、C三点的距离和为40个单位?
(3)当甲到A、B、C三点的距离和为40个单位时,甲调头返回,当甲、乙在数轴上再次相遇时,相遇点表示的数是 .
用边长为12cm的正方形硬纸板做三棱柱盒子,每个盒子的侧面为长方形,底面为等边三角形.
(1)每个盒子需 个长方形, 个等边三角形;
(2)硬纸板以如图两种方法裁剪(裁剪后边角料不再利用)A方法:剪6个侧面;B方法:剪4侧面5个底面.
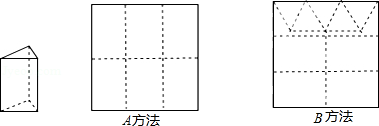
现有19张硬纸板,裁剪时x张用A方法,其余用B方法.
①用x的代数式分别表示裁剪出的侧面和底面的个数;
②若裁剪出的侧面和底面恰好全部用完,问能做多少个盒子?
如图,在数轴上点A表示的数为a,点B表示的数为b,且a,b满足|a+2|+(3a+b)2=0,O为原点.

(1)则a= ,b= ;
(2)若动点P从点A出发,以每秒1个单位长度的速度沿数轴向右匀速运动,
①当PO=2PB时,求点P的运动时间t;
②当点P运动到线段OB上时,分别取AP和OB的中点E、F,则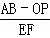 的值为 .
的值为 .
(3)有一动点Q从原点O出发第一次向左运动1个单位长度,然后在新的位置第二次运动,向右运动2个单位长度,在此位置第三次运动,向左运动3个单位长度…按照如此规律不断地左右运动,当运动到2015次时,求点Q所对应的有理数.
如图,点A从原点出发沿数轴向左运动,同时,点B也从原点出发沿数轴向右运动,3秒后,两点相距15个单位长度.已知点B的速度是点A的速度的4倍(速度单位:单位长度/秒).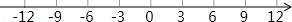
(1)求出点A、点B运动的速度,并在数轴上标出A、B两点从原点出发运动3秒时的位置;
(2)若A、B两点从(1)中的位置开始,仍以原来的速度同时沿数轴向左运动,几秒时,原点恰好处在点A、点B的正中间?
(3)若A、B两点从(1)中的位置开始,仍以原来的速度同时沿数轴向左运动时,另一点C同时从B点位置出发向A点运动,当遇到A点后,立即返回向B点运动,遇到B点后又立即返回向A点运动,如此往返,直到B点追上A点时,C点立即停止运动.若点C一直以20单位长度/秒的速度匀速运动,那么点C从开始运动到停止运动,行驶的路程是多少个单位长度?
家住山脚下的孔明同学想从家出发登山游玩,据以往的经验,他获得如下信息:
(1)他下山时的速度比上山时的速度每小时快1千米;
(2)他上山2小时到达的位置,离山顶还有1千米;
(3)抄近路下山,下山路程比上山路程近2千米;
(4)下山用1个小时;
根据上面信息,他作出如下计划:
(1)在山顶游览1个小时;
(2)中午12:00回到家吃中餐.
若依据以上信息和计划登山游玩,请问:孔明同学应该在什么时间从家出发?
试题篮
()