初中数学动点问题的函数图象试题

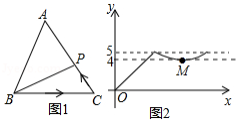
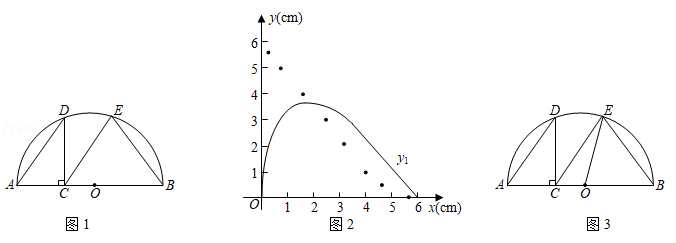
如图1，点从的顶点出发，沿匀速运动到点，图2是点运动时，线段的长度随时间变化的关系图象，其中为曲线部分的最低点，则的面积是　　．

如图，菱形 $\mathit{ABCD}$ 的边长为 $5\mathit{cm}$ ， $\sin A=\frac{4}{5}$ ，点 $P$ 从点 $A$ 出发，以 $1\mathit{cm}/s$ 的速度沿折线 $\mathit{AB}\to \mathit{BC}\to \mathit{CD}$ 运动，到达点 $D$ 停止；点 $Q$ 同时从点 $A$ 出发，以 $1\mathit{cm}/s$ 的速度沿 $\mathit{AD}$ 运动，到达点 $D$ 停止．设点 $P$ 运动 $x\left(s\right)$ 时， $\mathit{\Delta APQ}$ 的面积为 $y\left(c{m}^2\right)$ ，则能够反映 $y$ 与 $x$ 之间函数关系的图象是 $($ 　　 $)$

A．		B．
C．		D．

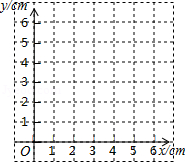
如图，是与弦所围成的图形的外部的一定点，是上一动点，连接交弦于点．

小腾根据学习函数的经验，对线段，，的长度之间的关系进行了探究．下面是小腾的探究过程，请补充完整：

（1）对于点在上的不同位置，画图、测量，得到了线段，，的长度的几组值，如下表：

	位置1	位置2	位置3	位置4	位置5	位置6	位置7	位置8
	3.44	3.30	3.07	2.70	2.25	2.25	2.64	2.83
	3.44	2.69	2.00	1.36	0.96	1.13	2.00	2.83
	0.00	0.78	1.54	2.30	3.01	4.00	5.11	6.00

在，，的长度这三个量中，确定　　的长度是自变量，　　的长度和　　的长度都是这个自变量的函数；

（2）在同一平面直角坐标系中，画出（1）中所确定的函数的图象；

（3）结合函数图象，解决问题：当时，的长度约为　　．

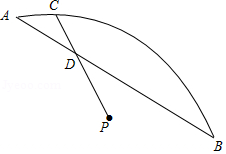
如图，是与弦所围成的图形的内部的一定点，是弦上一动点，连接并延长交于点，连接．已知，设，两点间的距离为，，两点间的距离为，，两点间的距离为．

小腾根据学习函数的经验，分别对函数，随自变量的变化而变化的规律进行了探究．

下面是小腾的探究过程，请补充完整：

（1）按照下表中自变量的值进行取点、画图、测量，分别得到了，与的几组对应值；

	0	1	2	3	4	5	6
	5.62	4.67	3.76		2.65	3.18	4.37
	5.62	5.59	5.53	5.42	5.19	4.73	4.11

（2）在同一平面直角坐标系中，描出补全后的表中各组数值所对应的点，，并画出函数，的图象；

（3）结合函数图象，解决问题：当为等腰三角形时，的长度约为　　．

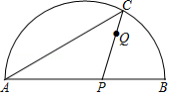
如图，是所对弦上一动点，过点作交于点，连接，过点作于点．已知，设、两点间的距离为，、两点间的距离为．（当点与点或点重合时，的值为

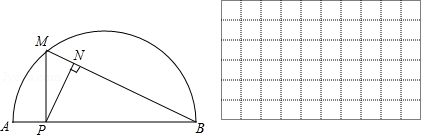
小东根据学习函数的经验，对函数随自变量的变化而变化的规律进行了探究．

下面是小东的探究过程，请补充完整：

（1）通过取点、画图、测量，得到了与的几组值，如下表：

	0	1	2	3	4	5	6
	0	2.0	2.3	2.1		0.9	0

（说明：补全表格时相关数值保留一位小数）

（2）建立平面直角坐标系，描出已补全后的表中各对对应值为坐标的点，画出该函数的图象．

（3）结合画出的函数图象，解决问题：当为等腰三角形时，的长度约为　　．

一段笔直的公路 $\mathit{AC}$ 长20千米，途中有一处休息点 $B$ ， $\mathit{AB}$ 长15千米，甲、乙两名长跑爱好者同时从点 $A$ 出发，甲以15千米 $/$ 时的速度匀速跑至点 $B$ ，原地休息半小时后，再以10千米 $/$ 时的速度匀速跑至终点 $C$ ；乙以12千米 $/$ 时的速度匀速跑至终点 $C$ ，下列选项中，能正确反映甲、乙两人出发后2小时内运动路程 $y$ （千米）与时间 $x$ （小时）函数关系的图象是 $($ 　　 $)$

A．		B．
C．		D．

如图， 中，，．点O是BC中点，点D沿B→A→C方向从B运动到C．设点D经过的路径长为，长为．则函数的图象大致为（  ）

如图1，点 $C$ 是半圆 $O$ 的直径 $\mathit{AB}$ 上一动点（不包括端点）， $\mathit{AB}=6\mathit{cm}$ ，过点 $C$ 作 $\mathit{CD}\perp \mathit{AB}$ 交半圆于点 $D$ ，连结 $\mathit{AD}$ ，过点 $C$ 作 $\mathit{CE}//\mathit{AD}$ 交半圆于点 $E$ ，连结 $\mathit{EB}$ ．牛牛想探究在点 $C$ 运动过程中 $\mathit{EC}$ 与 $\mathit{EB}$ 的大小关系．他根据学习函数的经验，记 $\mathit{AC}=\mathit{xcm}$ ， $\mathit{EC}=y_1\mathit{cm}$ ， $\mathit{EB}=y_2\mathit{cm}$ ．请你一起参与探究函数 $y_1$ 、 $y_2$ 随自变量 $x$ 变化的规律．

通过几何画板取点、画图、测量，得出如下几组对应值，并在图2中描出了以各对对应值为坐标的点，画出了不完整图象．

$x$	$\dots$	0.30	0.80	1.60	2.40	3.20	4.00	4.80	5.60	$\dots$
$y_1$	$\dots$	2.01	2.98	3.46	3.33	2.83	2.11	1.27	0.38	$\dots$
$y_2$	$\dots$	5.60	4.95	3.95	2.96	2.06	1.24	0.57	0.10	$\dots$

（1）当 $x=3$ 时， $y_1=$ 　　．

（2）在图2中画出函数 $y_2$ 的图象，并结合图象判断函数值 $y_1$ 与 $y_2$ 的大小关系．

（3）由（2）知" $\mathit{AC}$ 取某值时，有 $\mathit{EC}=\mathit{EB}$ "．如图3，牛牛连结了 $\mathit{OE}$ ，尝试通过计算 $\mathit{EC}$ ， $\mathit{EB}$ 的长来验证这一结论，请你完成计算过程．

如图，在菱形 $\mathit{ABCD}$ 中， $\mathit{AB}=2\mathit{cm}$ ， $\angle D=60°$ ，点 $P$ ， $Q$ 同时从点 $A$ 出发，点 $P$ 以 $1\mathit{cm}/s$ 的速度沿 $A-C-D$ 的方向运动，点 $Q$ 以 $2\mathit{cm}/s$ 的速度沿 $A-B-C-D$ 的方向运动，当其中一点到达 $D$ 点时，两点停止运动．设运动时间为 $x\left(s\right)$ ， $\mathit{\Delta APQ}$ 的面积为 $y\left(c{m}^2\right)$ ，则下列图象中能大致反映 $y$ 与 $x$ 之间函数关系的是 $($ 　　 $)$

A．
B．
C．
D．

如图，四边形 $\mathit{ABCD}$ 中，已知 $\mathit{AB}//\mathit{CD}$ ， $\mathit{AB}$ 与 $\mathit{CD}$ 之间的距离为4， $\mathit{AD}=5$ ， $\mathit{CD}=3$ ， $\angle \mathit{ABC}=45°$ ，点 $P$ ， $Q$ 同时由 $A$ 点出发，分别沿边 $\mathit{AB}$ ，折线 $\mathit{ADCB}$ 向终点 $B$ 方向移动，在移动过程中始终保持 $\mathit{PQ}\perp \mathit{AB}$ ，已知点 $P$ 的移动速度为每秒1个单位长度，设点 $P$ 的移动时间为 $x$ 秒， $\mathit{\Delta APQ}$ 的面积为 $y$ ，则能反映 $y$ 与 $x$ 之间函数关系的图象是 $($ 　　 $)$

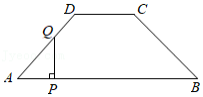
A．		B．
C．		D．

如图（1），在平面直角坐标系中，矩形 $\mathit{ABCD}$ 在第一象限，且 $\mathit{BC}//x$ 轴，直线 $y=2x+1$ 沿 $x$ 轴正方向平移，在平移过程中，直线被矩形 $\mathit{ABCD}$ 截得的线段长为 $a$ ，直线在 $x$ 轴上平移的距离为 $b$ ， $a$ 、 $b$ 间的函数关系图象如图（2）所示，那么矩形 $\mathit{ABCD}$ 的面积为 $($ 　　 $)$

A．

$\sqrt{5}$

B．

$2\sqrt{5}$

C．

8

D．

10

如图， $\mathit{\Delta OAB}$ 的顶点坐标分别为 $O(0,0)$ ， $A(3,4)$ ， $B(6,0)$ ，动点 $P$ 、 $Q$ 同时从点 $O$ 出发，分别沿 $x$ 轴正方向和 $y$ 轴正方向运动，速度分别为每秒3个单位和每秒2个单位，点 $P$ 到达点 $B$ 时点 $P$ 、 $Q$ 同时停止运动．过点 $Q$ 作 $\mathit{MN}//\mathit{OB}$ 分别交 $\mathit{AO}$ 、 $\mathit{AB}$ 于点 $M$ 、 $N$ ，连接 $\mathit{PM}$ 、 $\mathit{PN}$ ．设运动时间为 $t$ （秒 $)$ ．

（1）求点 $M$ 的坐标（用含 $t$ 的式子表示）；

（2）求四边形 $\mathit{MNBP}$ 面积的最大值或最小值；

（3）是否存在这样的直线 $l$ ，总能平分四边形 $\mathit{MNBP}$ 的面积？如果存在，请求出直线 $l$ 的解析式；如果不存在，请说明理由；

（4）连接 $\mathit{AP}$ ，当 $\angle \mathit{OAP}=\angle \mathit{BPN}$ 时，求点 $N$ 到 $\mathit{OA}$ 的距离．

如图1，菱形 $\mathit{ABCD}$ 的对角线 $\mathit{AC}$ 与 $\mathit{BD}$ 相交于点 $O$ ， $P$ 、 $Q$ 两点同时从 $O$ 点出发，以1厘米 $/$ 秒的速度在菱形的对角线及边上运动．点 $P$ 的运动路线为 $O-A-D-O$ ，点 $Q$ 的运动路线为 $O-C-B-O$ ．设运动的时间为 $x$ 秒， $P$ 、 $Q$ 间的距离为 $y$ 厘米， $y$ 与 $x$ 的函数关系的图象大致如图2所示，当点 $P$ 在 $A-D$ 段上运动且 $P$ 、 $Q$ 两点间的距离最短时， $P$ 、 $Q$ 两点的运动路程之和为 　　厘米．