初中数学一次函数的应用试题

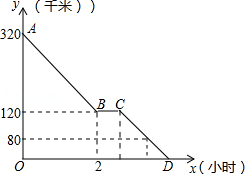
上周六上午8点，小颖同爸爸妈妈一起从西安出发回安康看望姥姥，途中他们在一个服务区休息了半小时，然后直达姥姥家，如图，是小颖一家这次行程中距姥姥家的距离 $y$ （千米）与他们路途所用的时间 $x$ （时 $)$ 之间的函数图象，请根据以上信息，解答下列问题：

（1）求直线 $\mathit{AB}$ 所对应的函数关系式；

（2）已知小颖一家出服务区后，行驶30分钟时，距姥姥家还有80千米，问小颖一家当天几点到达姥姥家？

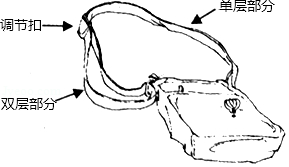
如图，是一种斜挎包，其挎带由双层部分、单层部分和调节扣构成．小敏用后发现，通过调节扣加长或缩短单层部分的长度，可以使挎带的长度（单层部分与双层部分长度的和，其中调节扣所占的长度忽略不计）加长或缩短．设单层部分的长度为，双层部分的长度为，经测量，得到如下数据：

单层部分的长度		4	6	8	10		150
双层部分的长度		73	72	71

（1）根据表中数据的规律，完成以下表格，并直接写出关于的函数解析式；

（2）根据小敏的身高和习惯，挎带的长度为时，背起来正合适，请求出此时单层部分的长度；

（3）设挎带的长度为，求的取值范围．

某公司推出一款产品，经市场调查发现，该产品的日销售量（个与销售单价（元之间满足一次函数关系关于销售单价，日销售量，日销售利润的几组对应值如表：

销售单价（元	85	95	105	115
日销售量（个	175	125	75
日销售利润（元	875	1875	1875	875

（注：日销售利润日销售量（销售单价成本单价）

（1）求关于的函数解析式（不要求写出的取值范围）及的值；

（2）根据以上信息，填空：

该产品的成本单价是　　元，当销售单价　　元时，日销售利润最大，最大值是　　元；

（3）公司计划开展科技创新，以降低该产品的成本，预计在今后的销售中，日销售量与销售单价仍存在（1）中的关系．若想实现销售单价为90元时，日销售利润不低于3750元的销售目标，该产品的成本单价应不超过多少元？

学校“百变魔方”社团准备购买，两种魔方，已知购买2个种魔方和6个种魔方共需130元，购买3个种魔方和4个种魔方所需款数相同．

（1）求这两种魔方的单价；

（2）结合社员们的需求，社团决定购买，两种魔方共100个（其中种魔方不超过50个）．某商店有两种优惠活动，如图所示．请根据以上信息，说明选择哪种优惠活动购买魔方更实惠．

某服装专卖店计划购进，两种型号的精品女装．已知2件型女装和3件型女装共需5600元；1件型女装和2件型女装共需3400元．

（1）求，型女装的单价

（2）专卖店购进，两种型号的女装共60件，其中型的件数不少于型件数的2倍，如果型女装打八折，那么该专卖店至少需要准备多少贷款？

学校准备购进一批节能灯，已知1只 $A$ 型节能灯和3只 $B$ 型节能灯共需26元；3只 $A$ 型节能灯和2只 $B$ 型节能灯共需29元．

（1）求一只 $A$ 型节能灯和一只 $B$ 型节能灯的售价各是多少元；

（2）学校准备购进这两种型号的节能灯共50只，并且 $A$ 型节能灯的数量不多于 $B$ 型节能灯数量的3倍，请设计出最省钱的购买方案，并说明理由．

为奖励在社会实践活动中表现优异的同学，某校准备购买一批文具袋和水性笔作为奖品．已知文具袋的单价是水性笔单价的5倍，购买5支水性笔和3个文具袋共需60元．

（1）求文具袋和水性笔的单价；

（2）学校准备购买文具袋10个，水性笔若干支（超过10支）．文具店给出两种优惠方案：

$A$ ：购买一个文具袋，赠送1支水性笔

$B$ ：购买水性笔10支以上，超出10支的部分按原价的八折优惠，文具袋不打折

①设购买水性笔 $x$ 支，选择方案 $A$ 的总费用为 $y_1$ 元，选择方案 $B$ 的总费用为 $y_2$ 元，分别求出 $y_1$ ， $y_2$ 与 $x$ 的函数关系式；

②该学校选择哪种方案更合算？请说明理由．

如图，在矩形中，，，为边上一点，，连接．动点、从点同时出发，点以的速度沿向终点运动；点以的速度沿折线向终点运动．设点运动的时间为，在运动过程中，点，点经过的路线与线段围成的图形面积为．

（1）　　，　　；

（2）求关于的函数解析式，并写出自变量的取值范围；

（3）当时，直接写出的值．

甲、乙两车分别从，两地同时出发，沿同一条公路相向行驶，相遇后，甲车继续以原速行驶到地，乙车立即以原速原路返回到地．甲、乙两车距地的路程与各自行驶的时间之间的关系如图所示．

（1）　　，　　；

（2）求乙车距地的路程关于的函数解析式，并写出自变量的取值范围；

（3）当甲车到达地时，求乙车距地的路程．

已知、两地之间有一条270千米的公路，甲、乙两车同时出发，甲车以60千米时的速度沿此公路从地匀速开往地，乙车从地沿此公路匀速开往地，两车分别到达目的地后停止．甲、乙两车相距的路程（千米）与甲车的行驶时间（时之间的函数关系如图所示．

（1）乙车的速度为　　千米时，　　，　　．

（2）求甲、乙两车相遇后与之间的函数关系式．

（3）当甲车到达距地70千米处时，求甲、乙两车之间的路程．

如图，在平面直角坐标系中，抛物线与轴相交于，两点，与轴相交于点，顶点为，直线与轴相交于点．

（1）当时，抛物线顶点的坐标为　　，　　；

（2）的长是否与值有关，说明你的理由；

（3）设，，求的取值范围；

（4）以为斜边，在直线的左下方作等腰直角三角形．设，直接写出关于的函数解析式及自变量的取值范围．

小玲和弟弟小东分别从家和图书馆同时出发，沿同一条路相向而行，小玲开始跑步中途改为步行，到达图书馆恰好用．小东骑自行车以的速度直接回家，两人离家的路程与各自离开出发地的时间之间的函数图象如图所示

（1）家与图书馆之间的路程为　　，小玲步行的速度为　　；

（2）求小东离家的路程关于的函数解析式，并写出自变量的取值范围；

（3）求两人相遇的时间．

某种水泥储存罐的容量为25立方米，它有一个输入口和一个输出口．从某时刻开始，只打开输入口，匀速向储存罐内注入水泥，3分钟后，再打开输出口，匀速向运输车输出水泥，又经过2.5分钟储存罐注满，关闭输入口，保持原来的输出速度继续向运输车输出水泥，当输出的水泥总量达到8立方米时，关闭输出口．储存罐内的水泥量（立方米）与时间（分之间的部分函数图象如图所示．

（1）求每分钟向储存罐内注入的水泥量．

（2）当时，求与之间的函数关系式．

（3）储存罐每分钟向运输车输出的水泥量是　　立方米，从打开输入口到关闭输出口共用的时间为　　分钟．

如图①，一个正方体铁块放置在圆柱形水槽内，现以一定的速度往水槽中注水，时注满水槽．水槽内水面的高度与注水时间之间的函数图象如图②所示．

（1）正方体的棱长为　　；

（2）求线段对应的函数解析式，并写出自变量的取值范围；

（3）如果将正方体铁块取出，又经过恰好将此水槽注满，直接写出的值．

甲、乙两车间同时开始加工一批服装．从开始加工到加工完这批服装甲车间工作了9小时，乙车间在中途停工一段时间维修设备，然后按停工前的工作效率继续加工，直到与甲车间同时完成这批服装的加工任务为止．设甲、乙两车间各自加工服装的数量为（件．甲车间加工的时间为（时，与之间的函数图象如图所示．

（1）甲车间每小时加工服装件数为　　件；这批服装的总件数为　　件．

（2）求乙车间维修设备后，乙车间加工服装数量与之间的函数关系式；

（3）求甲、乙两车间共同加工完1000件服装时甲车间所用的时间．