设抛物线的解析式为 ,过点 作 轴的垂线,交抛物线于点 ;过点 , 作 轴的垂线,交抛物线于点 ; ;过点 , 为正整数)作 轴的垂线,交抛物线于点 ,连接 ,得 △ .
(1)求 的值;
(2)直接写出线段 , 的长(用含 的式子表示);
(3)在系列 △ 中,探究下列问题:
①当 为何值时, △ 是等腰直角三角形?
②设 , 均为正整数),问:是否存在 △ 与 △ 相似?若存在,求出其相似比;若不存在,说明理由.
在平面直角坐标系中,
,
,
,
为抛物线
上任意两点,其中
.
(1)若抛物线的对称轴为,当
,
为何值时,
;
(2)设抛物线的对称轴为,若对于
,都有
,求
的取值范围.
如图1,已知抛物线y=-x2+bx+c经过点A(1,0),B(-3,0)两点,且与y轴交于点C.
(1)求b,c的值.
(2)在第二象限的抛物线上,是否存在一点P,使得△PBC的面积最大?求出点P的坐标及△PBC的面积最大值. 若不存在,请说明理由.
(3)如图2,点E为线段BC上一个动点(不与B,C重合),经过B、E、O三点的圆与过点B且垂直于BC的直线交于点F,当△OEF面积取得最小值时,求点E坐标.
如图,抛物线y=x2+bx+c与x轴交于A(-1,0)和B(3,0)两点,交y轴于E.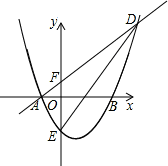
(1)求此抛物线的表达式.
(2)若直线y=x+1与抛物线交于A,D两点,与y轴交于点F,连接DE,求△DEF的面积.
已知抛物线y=ax2+bx+c与x轴交于点A(1,0),B(3,0),且过点C(0,-3).
(1)求抛物线的解析式和顶点坐标;
(2)请你写出一种平移的方法,使平移后抛物线的顶点落在直线y=-x上,并写出平移后抛物线的解析式.
在平面直角坐标系中,一个二次函数的图象经过点A(1,0)、B(3,0)两点.
(1)这个二次函数的对称轴是直线 ;
(2)设这个二次函数的顶点为D,与y轴交于点C,它的对称轴与x轴交于点E,连接AD、DE和DB,当△AOC与△DEB相似时,求这个二次函数的表达式。


(年云南省曲靖市)如图,在平面直角坐标系xOy中,直线l⊥y轴于点B(0,﹣2),A为OB的中点,以A为顶点的抛物线 与x轴交于C、D两点,且CD=4,点P为抛物线上的一个动点,以P为圆心,PO为半径画圆.
与x轴交于C、D两点,且CD=4,点P为抛物线上的一个动点,以P为圆心,PO为半径画圆.
(1)求抛物线的解析式;
(2)若⊙P与y轴的另一交点为E,且OE=2,求点P的坐标;
(3)判断直线l与⊙P的位置关系,并说明理由.
(年贵州省遵义市)如图,抛物线 (
( ≠0)与
≠0)与 轴交于A(-4,0),B(2,0),与
轴交于A(-4,0),B(2,0),与 轴交与点C(0,2).
轴交与点C(0,2).

(1)求抛物线的解析式;
(2)若点D为该抛物线上的一个动点,且在直线AC上方,当以A,C,D为顶点的三角形面积最大时,求点D的坐标及此时三角形的面积;(解题用图见答题卡)
(3)以AB为直径作⊙M,直线经过点E(-1,-5),并且与⊙M相切,求该直线的解析式.(解题用图见答题卡)
如图,直线AB交x轴于点B(4,0),交y轴于点A(0,4),直线DM⊥x轴正半轴于点M,交线段AB于点C,DM=6,连接DA,∠DAC=90°.
(1)直接写出直线AB的解析式;
(2)求点D的坐标;
(3)若点P是线段MB上的动点,过点P作x轴的垂线,交AB于点F,交过O、D、B三点的抛物线于点E,连接CE.是否存在点P,使△BPF与△FCE相似?若存在,请求出点P的坐标;若不存在,请说明理由.
已知抛物线y=ax2+bx+c(0<2a<b)的顶点为P(x0,y0),点A(1,yA)、B(0,yB)、C(-1,yC)在该抛物线上.
(Ⅰ)当a=1,b=4,c=10时,①求顶点P的坐标;②求-的值;
(Ⅱ)当y0≥0恒成立时,求的最小值.
设a、b是任意两个不等实数,我们规定:满足不等式a≤x≤b的实数x的所有取值的全体叫做闭区间,表示为[a,b].对于一个函数,如果它的自变量x与函数值y满足:当m≤x≤n时,有m≤y≤n,我们就称此函数是闭区间[m,n]上的“闭函数”.
(1)反比例函数 是闭区间[1,2014]上的“闭函数”吗?请判断并说明理由;
是闭区间[1,2014]上的“闭函数”吗?请判断并说明理由;
(2)若一次函数 是闭区间[m,n]上的“闭函数”,求此函数的解析式;
是闭区间[m,n]上的“闭函数”,求此函数的解析式;
(3)若二次函数 是闭区间[a,b]上的“闭函数”,求实数a,b的值.
是闭区间[a,b]上的“闭函数”,求实数a,b的值.
试题篮
()