初中数学二次函数的应用解答题

端午节是我国入选世界非物质文化遗产的传统节日，端午节吃粽子是中华民族的传统习俗．市场上豆沙粽的进价比猪肉粽的进价每盒便宜10元，某商家用8000元购进的猪肉粽和用6000元购进的豆沙粽盒数相同．在销售中，该商家发现猪肉粽每盒售价50元时，每天可售出100盒；每盒售价提高1元时，每天少售出2盒．

（1）求猪肉粽和豆沙粽每盒的进价；

（2）设猪肉粽每盒售价 $x$元 $(50⩽x⩽65)$， $y$表示该商家每天销售猪肉粽的利润（单位：元），求 $y$关于 $x$的函数解析式并求最大利润．

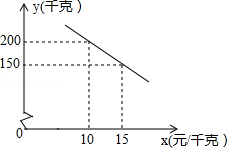
因疫情防控需要，消毒用品需求量增加．某药店新进一批桶装消毒液，每桶进价50元，每天销售量 $y$（桶 $)$与销售单价 $x$（元 $)$之间满足一次函数关系，其图象如图所示．

（1）求 $y$与 $x$之间的函数表达式；

（2）每桶消毒液的销售价定为多少元时，药店每天获得的利润最大，最大利润是多少元？（利润 $=$销售价 $-$进价）

某水果商店销售一种进价为40元 $/$千克的优质水果，若售价为50元 $/$千克，则一个月可售出500千克；若售价在50元 $/$千克的基础上每涨价1元，则月销售量就减少10千克．

（1）当售价为55元 $/$千克时，每月销售水果多少千克？

（2）当月利润为8750元时，每千克水果售价为多少元？

（3）当每千克水果售价为多少元时，获得的月利润最大？

用各种盛水容器可以制作精致的家用流水景观（如图 $1)$．

科学原理：如图2，始终盛满水的圆柱体水桶水面离地面的高度为 $H$（单位： $\mathit{cm})$，如果在离水面竖直距离为 $h$（单位： $\mathit{cm})$的地方开大小合适的小孔，那么从小孔射出水的射程（水流落地点离小孔的水平距离） $s$（单位： $\mathit{cm})$与 $h$的关系式为 $s^2=4h(H-h)$．

应用思考：现用高度为 $20\mathit{cm}$的圆柱体塑料水瓶做相关研究，水瓶直立地面，通过连续注水保证它始终盛满水，在离水面竖直距离 $\mathit{hcm}$处开一个小孔．

（1）写出 $s^2$与 $h$的关系式；并求出当 $h$为何值时，射程 $s$有最大值，最大射程是多少？

（2）在侧面开两个小孔，这两个小孔离水面的竖直距离分别为 $a$， $b$，要使两孔射出水的射程相同，求 $a$， $b$之间的关系式；

（3）如果想通过垫高塑料水瓶，使射出水的最大射程增加 $16\mathit{cm}$，求垫高的高度及小孔离水面的竖直距离．

如图1，排球场长为 $18m$，宽为 $9m$，网高为 $2.24m$，队员站在底线 $O$点处发球，球从点 $O$的正上方 $1.9m$的 $C$点发出，运动路线是抛物线的一部分，当球运动到最高点 $A$时，高度为 $2.88m$，即 $\mathit{BA}=2.88m$，这时水平距离 $\mathit{OB}=7m$，以直线 $\mathit{OB}$为 $x$轴，直线 $\mathit{OC}$为 $y$轴，建立平面直角坐标系，如图2．

（1）若球向正前方运动（即 $x$轴垂直于底线），求球运动的高度 $y\left(m\right)$与水平距离 $x\left(m\right)$之间的函数关系式（不必写出 $x$取值范围）．并判断这次发球能否过网？是否出界？说明理由．

（2）若球过网后的落点是对方场地①号位内的点 $P$（如图1，点 $P$距底线 $1m$，边线 $0.5m)$，问发球点 $O$在底线上的哪个位置？（参考数据： $\sqrt{2}$取 $1.4)$

如图1，在平面直角坐标系中， $\mathit{\Delta ABC}$的顶点 $A$， $C$分别是直线 $y=-\frac{8}{3}x+4$与坐标轴的交点，点 $B$的坐标为 $(-2,0)$，点 $D$是边 $\mathit{AC}$上的一点， $\mathit{DE}\perp \mathit{BC}$于点 $E$，点 $F$在边 $\mathit{AB}$上，且 $D$， $F$两点关于 $y$轴上的某点成中心对称，连结 $\mathit{DF}$， $\mathit{EF}$．设点 $D$的横坐标为 $m$， $E{F}^2$为 $l$，请探究：

①线段 $\mathit{EF}$长度是否有最小值．

② $\mathit{\Delta BEF}$能否成为直角三角形．

小明尝试用“观察 $-$猜想 $-$验证 $-$应用”的方法进行探究，请你一起来解决问题．

（1）小明利用“几何画板”软件进行观察，测量，得到 $l$随 $m$变化的一组对应值，并在平面直角坐标系中以各对应值为坐标描点（如图 $2)$．请你在图2中连线，观察图象特征并猜想 $l$与 $m$可能满足的函数类别．

（2）小明结合图1，发现应用三角形和函数知识能验证（1）中的猜想，请你求出 $l$关于 $m$的函数表达式及自变量的取值范围，并求出线段 $\mathit{EF}$长度的最小值．

（3）小明通过观察，推理，发现 $\mathit{\Delta BEF}$能成为直角三角形，请你求出当 $\mathit{\Delta BEF}$为直角三角形时 $m$的值．

在篮球比赛中，东东投出的球在点 $A$处反弹，反弹后球运动的路线为抛物线的一部分（如图1所示建立直角坐标系），抛物线顶点为点 $B$．

（1）求该抛物线的函数表达式．

（2）当球运动到点 $C$时被东东抢到， $\mathit{CD}\perp x$轴于点 $D$， $\mathit{CD}=2.6m$．

①求 $\mathit{OD}$的长．

②东东抢到球后，因遭对方防守无法投篮，他在点 $D$处垂直起跳传球，想将球沿直线快速传给队友华华，目标为华华的接球点 $E(4,1.3)$．东东起跳后所持球离地面高度 $h_1\left(m\right)$（传球前）与东东起跳后时间 $t\left(s\right)$满足函数关系式 $h_1=-2{(t-0.5)}^2+2.7(0⩽t⩽1)$；小戴在点 $F(1.5,0)$处拦截，他比东东晚 $0.3s$垂直起跳，其拦截高度 $h_2\left(m\right)$与东东起跳后时间 $t\left(s\right)$的函数关系如图2所示（其中两条抛物线的形状相同）．东东的直线传球能否越过小戴的拦截传到点 $E$？若能，东东应在起跳后什么时间范围内传球？若不能，请说明理由（直线传球过程中球运动时间忽略不计）．

如图（1）放置两个全等的含有 $30°$角的直角三角板 $\mathit{ABC}$与 $\mathit{DEF}(\angle B=\angle E=30°)$，若将三角板 $\mathit{ABC}$向右以每秒1个单位长度的速度移动（点 $C$与点 $E$重合时移动终止），移动过程中始终保持点 $B$、 $F$、 $C$、 $E$在同一条直线上，如图（2）， $\mathit{AB}$与 $\mathit{DF}$、 $\mathit{DE}$分别交于点 $P$、 $M$， $\mathit{AC}$与 $\mathit{DE}$交于点 $Q$，其中 $\mathit{AC}=\mathit{DF}=\sqrt{3}$，设三角板 $\mathit{ABC}$移动时间为 $x$秒．

（1）在移动过程中，试用含 $x$的代数式表示 $\mathit{\Delta AMQ}$的面积；

（2）计算 $x$等于多少时，两个三角板重叠部分的面积有最大值？最大值是多少？

“扬州漆器”名扬天下，某网店专门销售某种品牌的漆器笔筒，成本为30元 $/$件，每天销售 $y$（件 $)$与销售单价 $x$（元 $)$之间存在一次函数关系，如图所示．

（1）求 $y$与 $x$之间的函数关系式；

（2）如果规定每天漆器笔筒的销售量不低于240件，当销售单价为多少元时，每天获取的利润最大，最大利润是多少？

（3）该网店店主热心公益事业，决定从每天的销售利润中捐出150元给希望工程，为了保证捐款后每天剩余利润不低于3600元，试确定该漆器笔筒销售单价的范围．

如图，在平面直角坐标系中，一次函数 $y=-\frac{2}{3}x+4$的图象与 $x$轴和 $y$轴分别相交于 $A$、 $B$两点．动点 $P$从点 $A$出发，在线段 $\mathit{AO}$上以每秒3个单位长度的速度向点 $O$作匀速运动，到达点 $O$停止运动，点 $A$关于点 $P$的对称点为点 $Q$，以线段 $\mathit{PQ}$为边向上作正方形 $\mathit{PQMN}$．设运动时间为 $t$秒．

（1）当 $t=\frac{1}{3}$秒时，点 $Q$的坐标是　　；

（2）在运动过程中，设正方形 $\mathit{PQMN}$与 $\mathit{\Delta AOB}$重叠部分的面积为 $S$，求 $S$与 $t$的函数表达式；

（3）若正方形 $\mathit{PQMN}$对角线的交点为 $T$，请直接写出在运动过程中 $\mathit{OT}+\mathit{PT}$的最小值．

某景区商店销售一种纪念品，每件的进货价为40元．经市场调研，当该纪念品每件的销售价为50元时，每天可销售200件；当每件的销售价每增加1元，每天的销售数量将减少10件．

（1）当每件的销售价为52元时，该纪念品每天的销售数量为　　件；

（2）当每件的销售价 $x$为多少时，销售该纪念品每天获得的利润 $y$最大？并求出最大利润．

某乡镇实施产业扶贫，帮助贫困户承包了荒山种植某品种蜜柚，到了收获季节，已知该蜜柚的成本价为8元 $/$千克，投入市场销售时，调查市场行情，发现该蜜柚销售不会亏本，且每天销售量 $y$（千克）与销售单价 $x$（元 $/$千克）之间的函数关系如图所示．

（1）求 $y$与 $x$的函数关系式，并写出 $x$的取值范围；

（2）当该品种的蜜柚定价为多少时，每天销售获得的利润最大？最大利润是多少？

（3）某农户今年共采摘蜜柚4800千克，该品种蜜柚的保质期为40天，根据（2）中获得最大利润的方式进行销售，能否销售完这批蜜柚？请说明理由．

温州某企业安排65名工人生产甲、乙两种产品，每人每天生产2件甲或1件乙，甲产品每件可获利15元．根据市场需求和生产经验，乙产品每天产量不少于5件，当每天生产5件时，每件可获利120元，每增加1件，当天平均每件利润减少2元．设每天安排 $x$人生产乙产品．

（1）根据信息填表：

产品种类	每天工人数（人 $)$	每天产量（件 $)$	每件产品可获利润（元 $)$
甲			15
乙	$x$	$x$

（2）若每天生产甲产品可获得的利润比生产乙产品可获得的利润多550元，求每件乙产品可获得的利润．

（3）该企业在不增加工人的情况下，增加生产丙产品，要求每天甲、丙两种产品的产量相等．已知每人每天可生产1件丙（每人每天只能生产一件产品），丙产品每件可获利30元，求每天生产三种产品可获得的总利润 $W$（元 $)$的最大值及相应的 $x$值．

某药厂销售部门根据市场调研结果，对该厂生产的一种新型原料药未来两年的销售进行预测，并建立如下模型：设第 $t$个月该原料药的月销售量为 $P$（单位：吨）， $P$与 $t$之间存在如图所示的函数关系，其图象是函数 $P=\frac{120}{t+4}(0<t⩽8)$的图象与线段 $\mathit{AB}$的组合；设第 $t$个月销售该原料药每吨的毛利润为 $Q$（单位：万元）， $Q$与 $t$之间满足如下关系： $Q=\left\{\begin{array}{c}2t+8,0<t⩽12\\ -t+44,12<t⩽24\end{array}\right.$

（1）当 $8<t⩽24$时，求 $P$关于 $t$的函数解析式；

（2）设第 $t$个月销售该原料药的月毛利润为 $w$（单位：万元）

①求 $w$关于 $t$的函数解析式；

②该药厂销售部门分析认为， $336⩽w⩽513$是最有利于该原料药可持续生产和销售的月毛利润范围，求此范围所对应的月销售量 $P$的最小值和最大值．

学校拓展小组研制了绘图智能机器人（如图 $1)$，顺次输入点 $P_1$， $P_2$， $P_3$的坐标，机器人能根据图2，绘制图形．若图形是线段，求出线段的长度；若图形是抛物线，求出抛物线的函数关系式．请根据以下点的坐标，求出线段的长度或抛物线的函数关系式．

（1） $P_1(4,0)$， $P_2(0,0)$， $P_3(6,6)$；

（2） $P_1(0,0)$， $P_2(4,0)$， $P_3(6,6)$．