初中数学二次函数的应用试题

某商店销售一种商品，每件的进价为50元，经市场调研发现，当该商品每件的售价为60元时，每天可销售200件；当售价高于进价时，每件的售价每增加1元，每天的销售数量将减少10件．

（1）当每件商品的售价为64元时，求该商品每天的销售数量；

（2）当每件商品的售价为多少时，销售该商品每天获得的利润最大？并求出最大利润．

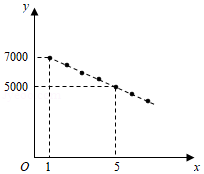
随着技术的发展，人们对各类产品的使用充满期待，某公司计划在某地区销售一款产品，根据市场分析，该产品的销售价格将随销售周期的变化而变化．设该产品在第为正整数）个销售周期每台的销售价格为元，与之间满足如图所示的一次函数关系．

（1）求与之间的关系式；

（2）设该产品在第个销售周期的销售数量为（万台），与的关系可以用来描述．根据以上信息，试问：哪个销售周期的销售收入最大？此时该产品每台的销售价格是多少元？

某商店销售一种商品，每件的进价为50元，经市场调研发现，当该商品每件的售价为60元时，每天可销售200件；当售价高于进价时，每件的售价每增加1元，每天的销售数量将减少10件．

（1）当每件商品的售价为64元时，求该商品每天的销售数量；

（2）当每件商品的售价为多少时，销售该商品每天获得的利润最大？并求出最大利润．

某农作物的生长率与温度有如下关系：如图，当时可近似用函数刻画；当时可近似用函数刻画．

（1）求的值．

（2）按照经验，该作物提前上市的天数（天与生长率之间满足已学过的函数关系，部分数据如下：

生长率	0.2	0.25	0.3	0.35
提前上市的天数（天	0	5	10	15

求：①关于的函数表达式；

②用含的代数式表示．

③天气寒冷，大棚加温可改变农作物生长速度．大棚恒温时每天的成本为100元，计划该作物30天后上市，现根据市场调查：每提前一天上市售出（一次售完），销售额可增加600元．因此决定给大棚继续加温，但加温导致成本增加，估测加温到时的成本为200元天，但若欲加温到，由于要采用特殊方法，成本增加到400元天．问加温到多少度时增加的利润最大？并说明理由．（注农作物上市售出后大棚暂停使用）

有一块形状如图的五边形余料，，，，，，要在这块余料中截取一块矩形材料，其中一条边在上，并使所截矩形材料的面积尽可能大．

（1）若所截矩形材料的一条边是或，求矩形材料的面积．

（2）能否截出比（1）中更大面积的矩形材料？如果能，求出这些矩形材料面积的最大值；如果不能，说明理由．

某宾馆有若干间标准房，当标准房的价格为200元时，每天入住的房间数为60间．经市场调查表明，该馆每间标准房的价格在元之间（含170元，240元）浮动时，每天入住的房间数（间与每间标准房的价格（元的数据如下表：

（元		190	200	210	220
（间		65	60	55	50

（1）根据所给数据在坐标系中描出相应的点，并画出图象．

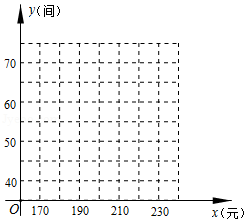
（2）求关于的函数表达式，并写出自变量的取值范围．

（3）设客房的日营业额为（元．若不考虑其他因素，问宾馆标准房的价格定为多少元时，客房的日营业额最大？最大为多少元？

某农作物的生长率与温度有如下关系：如图1，当时可近似用函数刻画；当时可近似用函数刻画．

（1）求的值．

（2）按照经验，该作物提前上市的天数（天与生长率满足函数关系：

生长率	0.2	0.25	0.3	0.35
提前上市的天数（天	0	5	10	15

①请运用已学的知识，求关于的函数表达式；

②请用含的代数式表示．

（3）天气寒冷，大棚加温可改变农作物生长速度．在（2）的条件下，原计划大棚恒温时，每天的成本为200元，该作物30天后上市时，根据市场调查：每提前一天上市售出（一次售完），销售额可增加600元．因此给大棚继续加温，加温后每天成本（元与大棚温度之间的关系如图2．问提前上市多少天时增加的利润最大？并求这个最大利润（农作物上市售出后大棚暂停使用）．

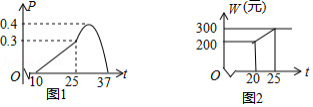
某驻村扶贫小组实施产业扶贫，帮助贫困农户进行西瓜种植和销售．已知西瓜的成本为6元千克，规定销售单价不低于成本，又不高于成本的两倍．经过市场调查发现，某天西瓜的销售量（千克）与销售单价（元千克）的函数关系如图所示：

（1）求与的函数解析式（也称关系式）；

（2）求这一天销售西瓜获得的利润的最大值．

某公司推出一款产品，经市场调查发现，该产品的日销售量（个与销售单价（元之间满足一次函数关系关于销售单价，日销售量，日销售利润的几组对应值如表：

销售单价（元	85	95	105	115
日销售量（个	175	125	75
日销售利润（元	875	1875	1875	875

（注：日销售利润日销售量（销售单价成本单价）

（1）求关于的函数解析式（不要求写出的取值范围）及的值；

（2）根据以上信息，填空：

该产品的成本单价是　　元，当销售单价　　元时，日销售利润最大，最大值是　　元；

（3）公司计划开展科技创新，以降低该产品的成本，预计在今后的销售中，日销售量与销售单价仍存在（1）中的关系．若想实现销售单价为90元时，日销售利润不低于3750元的销售目标，该产品的成本单价应不超过多少元？

如图，点 $E$ 、 $F$ 、 $G$ 、 $H$ 是正方形 $\mathit{ABCD}$ 四条边（不含端点）上的点， $\mathit{DE}=\mathit{AF}=\mathit{BG}=\mathit{CH}$ 设线段 $\mathit{DE}$ 的长为 $x\left(\mathit{cm}\right)$ ，四边形 $\mathit{EFGH}$ 的面积为 $y\left(c{m}^2\right)$ ，则能够反映 $y$ 与 $x$ 之间函数关系的图象大致是 $($ 　　 $)$

A．		B．
C．		D．

如图1，过点的抛物线与直线交于点．点是线段上一动点，过点作轴的垂线，垂足为点，交抛物线于点．设的面积为，点的横坐标为．

（1）请直接写出的值及抛物线的解析式．

（2）为探究最大时点的位置，甲、乙两同学结合图形给出如下解析：

甲：借助的长与三角形面积公式，求出关于的函数关系式，可确定点的位置．

乙：当点运动到点或点时，的值可看作0，则当点运动到中点时，最大，即最大时，点为的中点．

请参考甲的方法求出最大时点的坐标，进而判断乙的猜想是否正确，并说明理由．

（3）拓展探究：如图2，直线与任意抛物线相交于、两点，是线段上的一个动点，过点作抛物线对称轴的平行线，交该抛物线于点．当的面积最大时，点一定是线段的中点吗？试作出判断并说明理由．

如图，在矩形中，，．，两点分别从，同时出发，点沿折线运动，在上的速度是，在上的速度是；点在上以的速度向终点运动，过点作，垂足为点．连接，以，为邻边作．设运动的时间为，与矩形重叠部分的图形面积为

（1）当时，　　；

（2）求关于的函数解析式，并写出的取值范围；

（3）直线将矩形的面积分成两部分时，直接写出的值．

如图，在中，，，，动点从点出发，沿以每秒2个单位长度的速度向终点运动．过点作于点（点不与点、重合），作，边交射线于点．设点的运动时间为秒．

（1）用含的代数式表示线段的长；

（2）当点与点重合时，求的值；

（3）设与重叠部分图形的面积为，求与之间的函数关系式；

（4）当线段的垂直平分线经过一边中点时，直接写出的值．

如图，在中，，，．点从点出发，以的速度沿边向终点运动．过点作交折线于点，为中点，以为边向右侧作正方形．设正方形与重叠部分图形的面积是，点的运动时间为．

（1）当点在边上时，正方形的边长为　　（用含的代数式表示）；

（2）当点不与点重合时，求点落在边上时的值；

（3）当时，求关于的函数解析式；

（4）直接写出边的中点落在正方形内部时的取值范围．

如图①，在中，，，，点从点出发，沿折线向终点运动，在上以每秒5个单位长度的速度运动，在上以每秒3个单位长度的速度运动，点从点出发，沿方向以每秒个单位长度的速度运动，，两点同时出发，当点停止时，点也随之停止．设点运动的时间为秒．

（1）求线段的长；（用含的代数式表示）

（2）连结，当与的一边平行时，求的值；

（3）如图②，过点作于点，以，为邻边作矩形，点为的中点，连结．设矩形与重叠部分图形的面积为．①当点在线段上运动时，求与之间的函数关系式；②直接写出将矩形分成两部分的面积比为时的值．