某水果店在两周内,将标价为10元 斤的某种水果,经过两次降价后的价格为8.1元 斤,并且两次降价的百分率相同.
(1)求该种水果每次降价的百分率;
(2)从第一次降价的第1天算起,第 天( 为整数)的售价、销量及储存和损耗费用的相关信息如表所示.已知该种水果的进价为4.1元 斤,设销售该水果第 (天)的利润为 (元),求 与 之间的函数关系式,并求出第几天时销售利润最大?
时间 (天) |
|
|
|
售价(元 斤) |
第1次降价后的价格 |
第2次降价后的价格 |
|
销量(斤) |
|
|
|
储存和损耗费用(元) |
|
|
|
(3)在(2)的条件下,若要使第15天的利润比(2)中最大利润最多少127.5元,则第15天在第14天的价格基础上最多可降多少元?
俄罗斯世界杯足球赛期间,某商店销售一批足球纪念册,每本进价40元,规定销售单价不低于44元,且获利不高于 .试销售期间发现,当销售单价定为44元时,每天可售出300本,销售单价每上涨1元,每天销售量减少10本,现商店决定提价销售.设每天销售量为 本,销售单价为 元.
(1)请直接写出 与 之间的函数关系式和自变量 的取值范围;
(2)当每本足球纪念册销售单价是多少元时,商店每天获利2400元?
(3)将足球纪念册销售单价定为多少元时,商店每天销售纪念册获得的利润 元最大?最大利润是多少元?
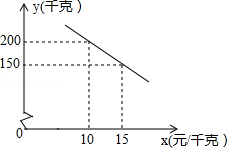
某乡镇实施产业扶贫,帮助贫困户承包了荒山种植某品种蜜柚,到了收获季节,已知该蜜柚的成本价为8元 千克,投入市场销售时,调查市场行情,发现该蜜柚销售不会亏本,且每天销售量 (千克)与销售单价 (元 千克)之间的函数关系如图所示.
(1)求 与 的函数关系式,并写出 的取值范围;
(2)当该品种的蜜柚定价为多少时,每天销售获得的利润最大?最大利润是多少?
(3)某农户今年共采摘蜜柚4800千克,该品种蜜柚的保质期为40天,根据(2)中获得最大利润的方式进行销售,能否销售完这批蜜柚?请说明理由.
【观察】 , , , , , , , , , , , , .
【发现】根据你的阅读回答问题:
(1)上述内容中,两数相乘,积的最大值为 ;
(2)设参与上述运算的第一个因数为 ,第二个因数为 ,用等式表示 与 的数量关系是 .
【类比】观察下列两数的积: , , , , , , , , , , .
猜想 的最大值为 ,并用你学过的知识加以证明.
某超市销售一种牛奶,进价为每箱24元,规定售价不低于进价.现在的售价为每箱36元,每月可销售60箱.市场调查发现:若这种牛奶的售价每降价1元,则每月的销量将增加10箱,设每箱牛奶降价 元 为正整数),每月的销量为 箱.
(1)写出 与 之间的函数关系式和自变量 的取值范围;
(2)超市如何定价,才能使每月销售牛奶的利润最大?最大利润是多少元?
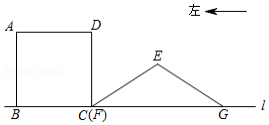
如图所示,在正方形 和 中, , ,点 、 、 、 在同一直线 上.当点 、 重合时, 以 的速度沿直线 向左开始运动, 秒后正方形 与 重合部分的面积为 .请解答下列问题:
(1)当 秒时,求 的值;
(2)当 秒时,求 的值;
(3)当5秒 秒时,求 与 的函数关系式,并求出 的最大值.
如图,已知 为 的直径, ,点 和点 是 上关于直线 对称的两个点,连接 、 ,且 ,直线 和直线 相交于点 ,过点 作直线 与线段 的延长线相交于点 ,与直线 相交于点 ,且 .
(1)求证:直线 为 的切线;
(2)若点 为线段 上一点,连接 ,满足 ,
① ;
②求 的最大值.

某广告公司设计一幅周长为16米的矩形广告牌,广告设计费为每平方米2000元.设矩形一边长为 x,面积为 S平方米.
(1)求 S与 x之间的函数关系式,并写出自变量 x的取值范围;
(2)设计费能达到24000元吗?为什么?
(3)当 x是多少米时,设计费最多?最多是多少元?
某商场试销 A、 B两种型号的台灯,下表是两次进货情况统计:
| 进货情况 进货次数 |
进货数量(台) |
进货资金(元) |
|
| A |
B |
||
| 第一次 |
5 |
3 |
230 |
| 第二次 |
10 |
4 |
440 |
(1)求 A、 B两种型号台灯的进价各为多少元?
(2)经试销发现, A型号台灯售价 x(元)与销售数量 y(台)满足关系式2 x+ y=140,此商场决定两种型号台灯共进货100台,并一周内全部售出,若 B型号台灯售价定为20元,求 A型号台灯售价定为多少时,商场可获得最大利润?并通过计算说明商场获得最大利润时的进货方案.
麦积山石窟是世界文化遗产,国家 级旅游景区,中国四大石窟之一.在2018年中国西北旅游营销大会暨旅游装备展上,商家按标价销售某种工艺品时,每件可获利45元;按标价的八五折销售该工艺品8件与将标价降低35元销售该工艺品12件所获利润相等.
(1)该工艺品每件的进价、标价分别是多少元?
(2)若每件工艺品按此进价进货、标价销售,商家每天可售出该工艺品100件;若每件工艺品降价1元,则每天可多售出该工艺品4件.问:每件工艺品降价多少元销售,每天获得的利润最大?获得的最大利润是多少元?
2016年12月29日至31日,黔南州第十届旅游产业发展大会在“中国长寿之乡” 罗甸县举行,从中寻找到商机的人不断涌现,促成了罗甸农民工返乡创业热潮.某“火龙果”经营户有 、 两种“火龙果”促销,若买2件 种“火龙果”和1件 种“火龙果”,共需120元;若买3件 种“火龙果”和2件 种“火龙果”,共需205元.
(1)设 , 两种“火龙果”每件售价分别为 元、 元,求 、 的值;
(2) 种“火龙果”每件的成本是40元,根据市场调查:若按(1)中求出的单价销售,该“火龙果”经营户每天销售 种“火龙果”100件;若销售单价每上涨1元, 种“火龙果”每天的销售量就减少5件.
①求每天 种“火龙果”的销售利润 (元 与销售单价 (元 之间的函数关系?
②求销售单价为多少元时, 种“火龙果”每天的销售利润最大,最大利润是多少?
六盘水市梅花山国际滑雪自建成以来,吸引大批滑雪爱好者,一滑雪者从山坡滑下,测得滑行距离 (单位: 与滑行时间 (单位: 之间的关系可以近似的用二次函数来表示.
滑行时间 |
0 |
1 |
2 |
3 |
|
滑行距离 |
0 |
4 |
12 |
24 |
|
(1)根据表中数据求出二次函数的表达式.现测量出滑雪者的出发点与终点的距离大约 ,他需要多少时间才能到达终点?
(2)将得到的二次函数图象补充完整后,向左平移2个单位,再向上平移5个单位,求平移后的函数表达式.
如图,利用一个直角墙角修建一个梯形储料场 ,其中 .若新建墙 与 总长为 ,则该梯形储料场 的最大面积是

A. B. C. D.
交通工程学理论把在单向道路上行驶的汽车看成连续的流体,并用流量、速度、密度三个概念描述车流的基本特征.其中流量 (辆 小时)指单位时间内通过道路指定断面的车辆数;速度 (千米 小时)指通过道路指定断面的车辆速度;密度 (辆 千米)指通过道路指定断面单位长度内的车辆数.
为配合大数据治堵行动,测得某路段流量 与速度 之间关系的部分数据如下表:
速度 (千米 小时) |
|
5 |
10 |
20 |
32 |
40 |
48 |
|
流量 (辆 小时) |
|
550 |
1000 |
1600 |
1792 |
1600 |
1152 |
|
(1)根据上表信息,下列三个函数关系式中,刻画 , 关系最准确的是 (只填上正确答案的序号)
① ;② ;③ .
(2)请利用(1)中选取的函数关系式分析,当该路段的车流速度为多少时,流量达到最大?最大流量是多少?
(3)已知 , , 满足 ,请结合(1)中选取的函数关系式继续解决下列问题.
①市交通运行监控平台显示,当 时道路出现轻度拥堵.试分析当车流密度 在什么范围时,该路段将出现轻度拥堵;
②在理想状态下,假设前后两车车头之间的距离 (米 均相等,求流量 最大时 的值.
试题篮
()