三孔桥横截面的三个孔都呈抛物线形,两小孔形状、大小完全相同.当水面刚好淹没小孔时,大孔水面宽度为10米,孔顶离水面1.5米;当水位下降,大孔水面宽度为14米时,单个小孔的水面宽度为4米,若大孔水面宽度为20米,则单个小孔的水面宽度为

A. 米B. 米C. 米D.7米
边长为 的正方形 中, 是对角线 上的一个动点(点 与 、 不重合),连接 ,将 绕点 顺时针旋转 到 ,连接 , 与 交于点 , 延长线与 (或 延长线)交于点 .
(1)连接 ,证明: ;
(2)设 , ,试写出 关于 的函数关系式,并求当 为何值时, ;
(3)猜想 与 的数量关系,并证明你的结论.

某游乐园有一个直径为16米的圆形喷水池,喷水池的周边有一圈喷水头,喷出的水柱为抛物线,在距水池中心3米处达到最高,高度为5米,且各方向喷出的水柱恰好在喷水池中心的装饰物处汇合.如图所示,以水平方向为 轴,喷水池中心为原点建立直角坐标系.
(1)求水柱所在抛物线(第一象限部分)的函数表达式;
(2)王师傅在喷水池内维修设备期间,喷水管意外喷水,为了不被淋湿,身高1.8米的王师傅站立时必须在离水池中心多少米以内?
(3)经检修评估,游乐园决定对喷水设施做如下设计改进:在喷出水柱的形状不变的前提下,把水池的直径扩大到32米,各方向喷出的水柱仍在喷水池中心保留的原装饰物(高度不变)处汇合,请探究扩建改造后喷水池水柱的最大高度.
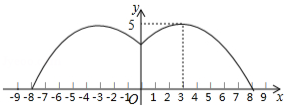
我市某超市销售一种文具,进价为5元 件.售价为6元 件时,当天的销售量为100件.在销售过程中发现:售价每上涨0.5元,当天的销售量就减少5件.设当天销售单价统一为 元 件 ,且 是按0.5元的倍数上涨),当天销售利润为 元.
(1)求 与 的函数关系式(不要求写出自变量的取值范围);
(2)要使当天销售利润不低于240元,求当天销售单价所在的范围;
(3)若每件文具的利润不超过 ,要想当天获得利润最大,每件文具售价为多少元?并求出最大利润.
2016年3月国际风筝节在铜仁市万山区举办,王大伯决定销售一批风筝,经市场调研:蝙蝠型风筝进价每个为10元,当售价每个为12元时,销售量为180个,若售价每提高1元,销售量就会减少10个,请回答以下问题:
(1)用表达式表示蝙蝠型风筝销售量 (个 与售价 (元 之间的函数关系 ;
(2)王大伯为了让利给顾客,并同时获得840元利润,售价应定为多少?
(3)当售价定为多少时,王大伯获得利润最大,最大利润是多少?
如图1,在矩形ABCD中,动点E从A出发,沿AB→BC方向运动,当点E到达点C时停止运动,过点E做FE⊥AE,交CD于F点,设点E运动路程为x,FC=y,如图2所表示的是y与x的函数关系的大致图象,当点E在BC上运动时,FC的最大长度是 ,则矩形ABCD的面积是( )
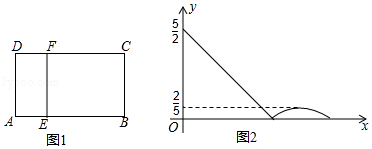
A. B.5C.6D.
某公司销售一种商品,成本为每件30元,经过市场调查发现,该商品的日销售量 (件 与销售单价 (元 是一次函数关系,其销售单价、日销售量的三组对应数值如下表:
| 销售单价 (元) |
40 |
60 |
80 |
| 日销售量 (件) |
80 |
60 |
40 |
(1)直接写出 与 的关系式 ;
(2)求公司销售该商品获得的最大日利润;
(3)销售一段时间以后,由于某种原因,该商品每件成本增加了10元,若物价部门规定该商品销售单价不能超过 元,在日销售量 (件 与销售单价 (元 保持(1)中函数关系不变的情况下,该商品的日销售最大利润是1500元,求 的值.
如图, 中, , , ,点 从点 出发,沿边 以 的速度向终点 运动,过点 作 ,交边 (或 于点 .设点 的运动时间为 , 的面积为 .

(1)当点 与点 重合时,求 的值;
(2)求 关于 的函数解析式,并直接写出自变量 的取值范围.
某公司计划从甲、乙两种产品中选择一种生产并销售,每年产销x件.已知产销两种产品的有关信息如表:
产品 |
每件售价(万元) |
每件成本(万元) |
每年其他费用(万元) |
每年最大产销量(件) |
甲 |
6 |
a |
20 |
200 |
乙 |
20 |
10 |
40+0.05x2 |
80 |
其中a为常数,且 。
(1)若产销甲、乙两种产品的年利润分别为y1万元、y2万元,直接写出y1、y2与x的函数关系式;
(2)分别求出产销两种产品的最大年利润;
(3)为获得最大年利润,该公司应该选择产销哪种产品?请说明理由.
当今,越来越多的青少年在观看影片《流浪地球》后,更加喜欢同名科幻小说,该小说销量也急剧上升.书店为满足广大顾客需求,订购该科幻小说若干本,每本进价为20元.根据以往经验:当销售单价是25元时,每天的销售量是250本;销售单价每上涨1元,每天的销售量就减少10本,书店要求每本书的利润不低于10元且不高于18元.
(1)直接写出书店销售该科幻小说时每天的销售量 y(本)与销售单价 x(元)之间的函数关系式及自变量的取值范围.
(2)书店决定每销售1本该科幻小说,就捐赠 a(0< a≤6)元给困难职工,每天扣除捐赠后可获得最大利润为1960元,求 a的值.
某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边用长为30米的篱笆围成,已知墙长为18米(如图所示),设这个苗圃园垂直于墙的一边的长为 米.
(1)若苗圃园的面积为72平方米,求 ;
(2)若平行于墙的一边长不小于8米,这个苗圃园的面积有最大值和最小值吗?如果有,求出最大值和最小值;如果没有,请说明理由;
(3)当这个苗圃园的面积不小于100平方米时,直接写出 的取值范围.

如图,利用一个直角墙角修建一个梯形储料场 ,其中 .若新建墙 与 总长为 ,则该梯形储料场 的最大面积是

A. B. C. D.
交通工程学理论把在单向道路上行驶的汽车看成连续的流体,并用流量、速度、密度三个概念描述车流的基本特征.其中流量 (辆 小时)指单位时间内通过道路指定断面的车辆数;速度 (千米 小时)指通过道路指定断面的车辆速度;密度 (辆 千米)指通过道路指定断面单位长度内的车辆数.
为配合大数据治堵行动,测得某路段流量 与速度 之间关系的部分数据如下表:
速度 (千米 小时) |
|
5 |
10 |
20 |
32 |
40 |
48 |
|
流量 (辆 小时) |
|
550 |
1000 |
1600 |
1792 |
1600 |
1152 |
|
(1)根据上表信息,下列三个函数关系式中,刻画 , 关系最准确的是 (只填上正确答案的序号)
① ;② ;③ .
(2)请利用(1)中选取的函数关系式分析,当该路段的车流速度为多少时,流量达到最大?最大流量是多少?
(3)已知 , , 满足 ,请结合(1)中选取的函数关系式继续解决下列问题.
①市交通运行监控平台显示,当 时道路出现轻度拥堵.试分析当车流密度 在什么范围时,该路段将出现轻度拥堵;
②在理想状态下,假设前后两车车头之间的距离 (米 均相等,求流量 最大时 的值.
试题篮
()