初中数学二次函数的应用试题

东坡商贸公司购进某种水果的成本为20元/kg，经过市场调研发现，这种水果在未来48天的销售单价p（元/kg）与时间t（天）之间的函数关系式为 $p=\left\{\begin{array}{c}\frac{1}{4}t+30(1\le t\le 24,t\mathit{为整数）}\\ \text{-}\frac{\text{1}}{\text{2}}t+48(25\le t\le 48,t\mathit{为整数})\end{array}\right.$，且其日销售量y（kg）与时间t（天）的关系如表：

时间t（天）	1	3	6	10	20	40	…
日销售量y（kg）	118	114	108	100	80	40	…

（1）已知y与t之间的变化规律符合一次函数关系，试求在第30天的日销售量是多少？

（2）问哪一天的销售利润最大？最大日销售利润为多少？

（3）在实际销售的前24天中，公司决定每销售1kg水果就捐赠n元利润（n＜9）给“精准扶贫”对象．现发现：在前24天中，每天扣除捐赠后的日销售利润随时间t的增大而增大，求n的取值范围．

如图，在 $\text{Rt}\Delta \text{ABC}$中， $\angle A=90°$． $\mathit{AB}=8\mathit{cm}$， $\mathit{AC}=6\mathit{cm}$，若动点 $D$从 $B$出发，沿线段 $\mathit{BA}$运动到点 $A$为止（不考虑 $D$与 $B$， $A$重合的情况），运动速度为 $2\mathit{cm}/s$，过点 $D$作 $\mathit{DE}//\mathit{BC}$交 $\mathit{AC}$于点 $E$，连接 $\mathit{BE}$，设动点 $D$运动的时间为 $x\left(s\right)$， $\mathit{AE}$的长为 $y\left(\mathit{cm}\right)$．

（1）求 $y$关于 $x$的函数表达式，并写出自变量 $x$的取值范围；

（2）当 $x$为何值时， $\mathit{\Delta BDE}$的面积 $S$有最大值？最大值为多少？

某宾馆有客房50间，当每间客房每天的定价为220元时，客房会全部住满；当每间客房每天的定价增加10元时，就会有一间客房空闲，设每间客房每天的定价增加x元时，客房入住数为y间．

（1）求y与x的函数关系式（不要求写出x的取值范围）；

（2）如果每间客房入住后每天的各种支出为40元，不考虑其他因素，则该宾馆每间客房每天的定价为多少时利润最大？

对某条线段的长度进行了3次测量，得到3个结果（单位：，10.1，10.0，若用作为这条线段长度的近似值，当　 　时，最小．对另一条线段的长度进行了次测量，得到个结果（单位：，，，，若用作为这条线段长度的近似值，当　　时，最小．

某广告公司设计一幅周长为16米的矩形广告牌，广告设计费为每平方米2000元．设矩形一边长为 x，面积为 S平方米．

（1）求 S与 x之间的函数关系式，并写出自变量 x的取值范围；

（2）设计费能达到24000元吗？为什么？

（3）当 x是多少米时，设计费最多？最多是多少元？

在一空旷场地上设计一落地为矩形 $\mathit{ABCD}$的小屋， $\mathit{AB}+\mathit{BC}=10m$，拴住小狗的 $10m$长的绳子一端固定在 $B$点处，小狗在不能进入小屋内的条件下活动，其可以活动的区域面积为 $S\left(m^2\right)$．

（1）如图1，若 $\mathit{BC}=4m$，则 $S=$　　 $m^2$．

（2）如图2，现考虑在（1）中的矩形 $\mathit{ABCD}$小屋的右侧以 $\mathit{CD}$为边拓展一正 $\mathit{\Delta CDE}$区域，使之变成落地为五边形 $\mathit{ABCED}$的小屋，其他条件不变，则在 $\mathit{BC}$的变化过程中，当 $S$取得最小值时，边 $\mathit{BC}$的长为　　 $m$．

"互联网 $+$ "时代，网上购物备受消费者青睐．某网店专售一款休闲裤，其成本为每条40元，当售价为每条80元时，每月可销售100条．为了吸引更多顾客，该网店采取降价措施．据市场调查反映：销售单价每降1元，则每月可多销售5条．设每条裤子的售价为 $x$ 元 $(x$ 为正整数），每月的销售量为 $y$ 条．

（1）直接写出 $y$ 与 $x$ 的函数关系式；

（2）设该网店每月获得的利润为 $w$ 元，当销售单价降低多少元时，每月获得的利润最大，最大利润是多少？

（3）该网店店主热心公益事业，决定每月从利润中捐出200元资助贫困学生．为了保证捐款后每月利润不低于4220元，且让消费者得到最大的实惠，该如何确定休闲裤的销售单价？

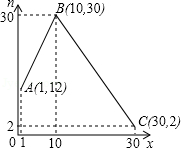
为落实“精准扶贫”精神，市农科院专家指导李大爷利用坡前空地种植优质草莓．根据场调查，在草莓上市销售的30天中，其销售价格（元公斤）与第天之间满足为正整数），销售量（公斤）与第天之间的函数关系如图所示：

如果李大爷的草莓在上市销售期间每天的维护费用为80元．

（1）求销售量与第天之间的函数关系式；

（2）求在草莓上市销售的30天中，每天的销售利润与第天之间的函数关系式；（日销售利润日销售额日维护费）

（3）求日销售利润的最大值及相应的．

有一块矩形地块 $\mathit{ABCD}$ ， $\mathit{AB}=20$ 米， $\mathit{BC}=30$ 米．为美观，拟种植不同的花卉，如图所示，将矩形 $\mathit{ABCD}$ 分割成四个等腰梯形及一个矩形，其中梯形的高相等，均为 $x$ 米．现决定在等腰梯形 $\mathit{AEHD}$ 和 $\mathit{BCGF}$ 中种植甲种花卉；在等腰梯形 $\mathit{ABFE}$ 和 $\mathit{CDHG}$ 中种植乙种花卉；在矩形 $\mathit{EFGH}$ 中种植丙种花卉．甲、乙、丙三种花卉的种植成本分别为20元 $/$ 米 ${}^2$ 、60元 $/$ 米 ${}^2$ 、40元 $/$ 米 ${}^2$ ，设三种花卉的种植总成本为 $y$ 元．

（1）当 $x=5$ 时，求种植总成本 $y$ ；

（2）求种植总成本 $y$ 与 $x$ 的函数表达式，并写出自变量 $x$ 的取值范围；

（3）若甲、乙两种花卉的种植面积之差不超过120平方米，求三种花卉的最低种植总成本．

某水果超市以每千克20元的价格购进一批樱桃，规定每千克樱桃售价不低于进价又不高于40元，经市场调查发现，樱桃的日销售量 $y$ （千克）与每千克售价 $x$ （元 $)$ 满足一次函数关系，其部分对应数据如下表所示：

每千克售价     $x$ （元     $)$	$\dots$	25	30	35	$\dots$
日销售量     $y$ （千克）	$\dots$	110	100	90	$\dots$

（1）求 $y$ 与 $x$ 之间的函数关系式；

（2）该超市要想获得1000的日销售利润，每千克樱桃的售价应定为多少元？

（3）当每千克樱桃的售价定为多少元时，日销售利润最大？最大利润是多少？

小红经营的网店以销售文具为主，其中一款笔记本进价为每本10元，该网店在试销售期间发现，每周销售数量 $y$ （本 $)$ 与销售单价 $x$ （元 $)$ 之间满足一次函数关系，三对对应值如下表：

销售单价     $x$ （元     $)$	12	14	16
每周的销售量     $y$ （本     $)$	500	400	300

（1）求 $y$ 与 $x$ 之间的函数关系式；

（2）通过与其他网店对比，小红将这款笔记本的单价定为 $x$ 元 $(12⩽x⩽15$ ，且 $x$ 为整数），设每周销售该款笔记本所获利润为 $w$ 元，当销售单价定为多少元时每周所获利润最大，最大利润是多少元？

如图，在平面直角坐标系中，已知 A（﹣3，﹣2）， B（0，﹣2）， C（﹣3，0）， M是线段 AB上的一个动点，连接 CM，过点 M作 MN⊥ MC交 y轴于点 N，若点 M、 N在直线 y＝ kx+ b上，则 b的最大值是（　　）

A．

﹣ $\frac{7}{8}$

B．

﹣ $\frac{3}{4}$

C．

﹣1

D．

0

交通工程学理论把在单向道路上行驶的汽车看成连续的流体，并用流量、速度、密度三个概念描述车流的基本特征．其中流量 $q$（辆 $/$小时）指单位时间内通过道路指定断面的车辆数；速度 $v$（千米 $/$小时）指通过道路指定断面的车辆速度；密度 $k$（辆 $/$千米）指通过道路指定断面单位长度内的车辆数．

为配合大数据治堵行动，测得某路段流量 $q$与速度 $v$之间关系的部分数据如下表：

速度 $v$（千米 $/$小时）	$\dots$	5	10	20	32	40	48	$\dots$
流量 $q$（辆 $/$小时）	$\dots$	550	1000	1600	1792	1600	1152	$\dots$

（1）根据上表信息，下列三个函数关系式中，刻画 $q$， $v$关系最准确的是　　（只填上正确答案的序号）

① $q=90v+100$；② $q=\frac{32000}{v}$；③ $q=-2v^2+120v$．

（2）请利用（1）中选取的函数关系式分析，当该路段的车流速度为多少时，流量达到最大？最大流量是多少？

（3）已知 $q$， $v$， $k$满足 $q=\mathit{vk}$，请结合（1）中选取的函数关系式继续解决下列问题．

①市交通运行监控平台显示，当 $12⩽v<18$时道路出现轻度拥堵．试分析当车流密度 $k$在什么范围时，该路段将出现轻度拥堵；

②在理想状态下，假设前后两车车头之间的距离 $d$（米 $)$均相等，求流量 $q$最大时 $d$的值．

如图，在边长为 $6\mathit{cm}$的正方形 $\mathit{ABCD}$中，点 $E$、 $F$、 $G$、 $H$分别从点 $A$、 $B$、 $C$、 $D$同时出发，均以 $1\mathit{cm}/s$的速度向点 $B$、 $C$、 $D$、 $A$匀速运动，当点 $E$到达点 $B$时，四个点同时停止运动，在运动过程中，当运动时间为　     　 $s$时，四边形 $\mathit{EFGH}$的面积最小，其最小值是　     　 $c{m}^2$．

某厂商投产一种新型科技产品，每件制造成本为18元，试销过程中发现，每月销售量 y（万件）与销售单价 x（元）之间的关系可以近似地看作一次函数 y＝﹣2 x+100

（1）写出每月的利润 L（万元）与销售单价 x（元）之间的函数关系式；

（2）当销售单价为多少元时，厂商每月能获得312万元的利润？当销售单价为多少元时，厂商每月能获得最大利润？最大利润是多少？

（3）根据相关部门规定，这种科技产品的销售单价不能高于32元，如果厂商要获得每月不低于312万元的利润，那么制造出这种产品每月的最低制造成本需要多少万元？