某商店原来平均每天可销售某种水果200千克,每千克可盈利6元,为减少库存,经市场调查,如果这种水果每千克降价1元,则每天可多售出20千克.
(1)设每千克水果降价x元,平均每天盈利y元,试写出y关于x的函数表达式;
(2)若要平均每天盈利960元,则每千克应降价多少元?
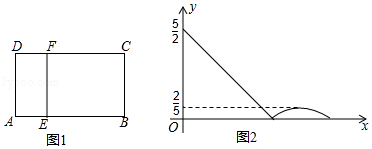
已知矩形 中, ,点 为对角线 上的一点,且 .如图①,动点 从点 出发,在矩形边上沿着 的方向匀速运动(不包含点 ).设动点 的运动时间为 , 的面积为 , 与 的函数关系如图②所示.
(1)直接写出动点 的运动速度为 , 的长度为 ;
(2)如图③,动点 重新从点 出发,在矩形边上按原来的速度和方向匀速运动,同时,另一个动点 从点 出发,在矩形边上沿着 的方向匀速运动,设动点 的运动速度为 .已知两动点 , 经过时间 在线段 上相遇(不包含点 ),动点 , 相遇后立即同时停止运动,记此时 与 的面积分别为 ,
①求动点 运动速度 的取值范围;
②试探究 是否存在最大值,若存在,求出 的最大值并确定运动时间 的值;若不存在,请说明理由.

如图1,在矩形ABCD中,动点E从A出发,沿AB→BC方向运动,当点E到达点C时停止运动,过点E做FE⊥AE,交CD于F点,设点E运动路程为x,FC=y,如图2所表示的是y与x的函数关系的大致图象,当点E在BC上运动时,FC的最大长度是 ,则矩形ABCD的面积是( )
A. B.5C.6D.
小明家的洗手盆上装有一种抬启式水龙头(如图 ,完全开启后,水流路线呈抛物线,把手端点 ,出水口 和落水点 恰好在同一直线上,点 至出水管 的距离为 ,洗手盆及水龙头的相关数据如图2所示,现用高 的圆柱型水杯去接水,若水流所在抛物线经过点 和杯子上底面中心 ,则点 到洗手盆内侧的距离 为 .

某工厂制作 A, B两种手工艺品, B每件获利比 A多105元,获利30元的 A与获利240元的 B数量相等.
(1)制作一件 A和一件 B分别获利多少元?
(2)工厂安排65人制作 A, B两种手工艺品,每人每天制作2件 A或1件 B.现在在不增加工人的情况下,增加制作 C.已知每人每天可制作1件 C(每人每天只能制作一种手工艺品),要求每天制作 A, C两种手工艺品的数量相等.设每天安排 x人制作 B, y人制作 A,写出 y与 x之间的函数关系式.
(3)在(1)(2)的条件下,每天制作 B不少于5件.当每天制作5件时,每件获利不变.若每增加1件,则当天平均每件获利减少2元.已知 C每件获利30元,求每天制作三种手工艺品可获得的总利润 W(元)的最大值及相应 x的值.
如图,利用一个直角墙角修建一个梯形储料场 ,其中 .若新建墙 与 总长为 ,则该梯形储料场 的最大面积是

A. B. C. D.
某企业接到生产一批设备的订单,要求不超过12天完成.这种设备的出厂价为1200元 台,该企业第一天生产22台设备,第二天开始,每天比前一天多生产2台.若干天后,每台设备的生产成本将会增加,设第 天 为整数)的生产成本为 (元 台), 与 的关系如图所示.
(1)若第 天可以生产这种设备 台,则 与 的函数关系式为 , 的取值范围为 ;
(2)第几天时,该企业当天的销售利润最大?最大利润为多少?
(3)求当天销售利润低于10800元的天数.

2020年新冠肺炎疫情期间,部分药店趁机将口罩涨价,经调查发现某药店某月(按30天计)前5天的某型号口罩销售价格 (元 只)和销量 (只 与第 天的关系如下表:
| 第 天 |
1 |
2 |
3 |
4 |
5 |
| 销售价格 (元 只) |
2 |
3 |
4 |
5 |
6 |
| 销量 (只 |
70 |
75 |
80 |
85 |
90 |
物价部门发现这种乱象后,统一规定各药店该型号口罩的销售价格不得高于1元 只,该药店从第6天起将该型号口罩的价格调整为1元 只.据统计,该药店从第6天起销量 (只 与第 天的关系为 ,且 为整数),已知该型号口罩的进货价格为0.5元 只.
(1)直接写出该药店该月前5天的销售价格 与 和销量 与 之间的函数关系式;
(2)求该药店该月销售该型号口罩获得的利润 (元 与 的函数关系式,并判断第几天的利润最大;
(3)物价部门为了进一步加强市场整顿,对此药店在这个月销售该型号口罩的过程中获得的正常利润之外的非法所得部分处以 倍的罚款,若罚款金额不低于2000元,则 的取值范围为 .
某超市销售一款"免洗洗手液",这款"免洗洗手液"的成本价为每瓶16元,当销售单价定为20元时,每天可售出80瓶.根据市场行情,现决定降价销售.市场调查反映:销售单价每降低0.5元,则每天可多售出20瓶(销售单价不低于成本价),若设这款"免洗洗手液"的销售单价为 (元 ,每天的销售量为 (瓶 .
(1)求每天的销售量 (瓶 与销售单价 (元 之间的函数关系式;
(2)当销售单价为多少元时,销售这款"免洗洗手液"每天的销售利润最大,最大利润为多少元?
某商场试销 A、 B两种型号的台灯,下表是两次进货情况统计:
| 进货情况 进货次数 |
进货数量(台) |
进货资金(元) |
|
| A |
B |
||
| 第一次 |
5 |
3 |
230 |
| 第二次 |
10 |
4 |
440 |
(1)求 A、 B两种型号台灯的进价各为多少元?
(2)经试销发现, A型号台灯售价 x(元)与销售数量 y(台)满足关系式2 x+ y=140,此商场决定两种型号台灯共进货100台,并一周内全部售出,若 B型号台灯售价定为20元,求 A型号台灯售价定为多少时,商场可获得最大利润?并通过计算说明商场获得最大利润时的进货方案.
一茶叶专卖店经销某种品牌的茶叶,该茶叶的成本价是80元/kg,销售单价不低于120元/kg.且不高于180元/kg,经销一段时间后得到如下数据:
销售单价x(元/kg) |
120 |
130 |
… |
180 |
每天销量y(kg) |
100 |
95 |
… |
70 |
设y与x的关系是我们所学过的某一种函数关系.
(1)直接写出y与x的函数关系式,并指出自变量x的取值范围;
(2)当销售单价为多少时,销售利润最大?最大利润是多少?
某网店销售某款童装,每件售价60元,每星期可卖300件,为了促销,该网店决定降价销售.市场调查反映:每降价1元,每星期可多卖30件.已知该款童装每件成本价40元,设该款童装每件售价x元,每星期的销售量为y件.
(1)求y与x之间的函数关系式;
(2)当每件售价定为多少元时,每星期的销售利润最大,最大利润多少元?
(3)若该网店每星期想要获得不低于6480元的利润,每星期至少要销售该款童装多少件?
如图,在平面直角坐标系中,已知 A(﹣3,﹣2), B(0,﹣2), C(﹣3,0), M是线段 AB上的一个动点,连接 CM,过点 M作 MN⊥ MC交 y轴于点 N,若点 M、 N在直线 y= kx+ b上,则 b的最大值是( )

| A. |
﹣ |
B. |
﹣ |
C. |
﹣1 |
D. |
0 |
如图,在边长为 的正方形 中,点 、 、 、 分别从点 、 、 、 同时出发,均以 的速度向点 、 、 、 匀速运动,当点 到达点 时,四个点同时停止运动,在运动过程中,当运动时间为 时,四边形 的面积最小,其最小值是 .

某厂商投产一种新型科技产品,每件制造成本为18元,试销过程中发现,每月销售量 y(万件)与销售单价 x(元)之间的关系可以近似地看作一次函数 y=﹣2 x+100
(1)写出每月的利润 L(万元)与销售单价 x(元)之间的函数关系式;
(2)当销售单价为多少元时,厂商每月能获得312万元的利润?当销售单价为多少元时,厂商每月能获得最大利润?最大利润是多少?
(3)根据相关部门规定,这种科技产品的销售单价不能高于32元,如果厂商要获得每月不低于312万元的利润,那么制造出这种产品每月的最低制造成本需要多少万元?
试题篮
()