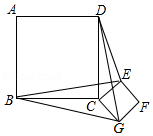
如图,正方形 的边长为4,点 、 分别从点 、点 以相同速度同时出发,点 从点 向点 运动,点 从点 向点 运动,点 运动到 点时, 、 停止运动.连接 、 相交于点 ,连接 .有下列结论:① ;②点 随着点 、 的运动而运动,且点 的运动路径的长度为 ;③线段 的最小值为 ;④当线段 最小时, 的面积 .其中正确的命题有 .(填序号)

如图,在平行四边形 中, , ,垂足分别为 , , , 分别与 交于点 和 ,且 .
(1)若 ,求 的长;
(2)求证: .

如图,正方形 中.点 , 分别在 , 上, 是等边三角形.连接 交 于点 .过点 作 于点 ,若 ,则

A.6B.4C.3D.2
如图,正方形 和正方形 边长分别为 和 ,正方形 绕点 旋转,给出下列结论:① ;② ;③ ,其中正确结论是 (填序号)
如图,点 是正方形 的边 延长线上一点,连接 ,过顶点 作 ,垂足为 , 分别交 于 ,交 于 .
(1)求证: ;
(2)若点 为 的中点,求 的值.

如图, 过 对角线的交点 ,交 于 ,交 于 ,若 的周长为18, ,则四边形 的周长为

A.14B.13C.12D.10
(1)操作发现:如图①,小明画了一个等腰三角形 ,其中 ,在 的外侧分别以 , 为腰作了两个等腰直角三角形 , ,分别取 , , 的中点 , , ,连接 , .小明发现了:线段 与 的数量关系是 ;位置关系是 .
(2)类比思考:
如图②,小明在此基础上进行了深入思考.把等腰三角形 换为一般的锐角三角形,其中 ,其它条件不变,小明发现的上述结论还成立吗?请说明理由.
(3)深入研究:
如图③,小明在(2)的基础上,又作了进一步的探究.向 的内侧分别作等腰直角三角形 , ,其它条件不变,试判断 的形状,并给与证明.

【问题解决】
一节数学课上,老师提出了这样一个问题:如图1,点 是正方形 内一点, , , .你能求出 的度数吗?
小明通过观察、分析、思考,形成了如下思路:
思路一:将 绕点 逆时针旋转 ,得到△ ,连接 ,求出 的度数;
思路二:将 绕点 顺时针旋转 ,得到△ ,连接 ,求出 的度数.
请参考小明的思路,任选一种写出完整的解答过程.
【类比探究】
如图2,若点 是正方形 外一点, , , ,求 的度数.

对角线长分别为6和8的菱形 如图所示,点 为对角线的交点,过点 折叠菱形,使 , 两点重合, 是折痕.若 ,则 的长为

A.7B.6C.5D.4
如图,点 是正方形 边 上一点,连接 ,作 于点 , 于点 ,连接 .
(1)求证: ;
(2)已知 ,四边形 的面积为24,求 的正弦值.
如图,正方形 的边长为1,点 与原点重合,点 在 轴的正半轴上,点 在 轴的负半轴上,将正方形 绕点 逆时针旋转 至正方形 的位置, 与 相交于点 ,则点 的坐标为 .

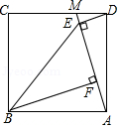
如图1,在四边形 中, , , ,垂足分别为 , , , ,点 , , 分别为 , , 的中点,连接 , , .

(1)如图2,当 , , 时,求 的值;
(2)若 , ,则可求出图中哪些线段的长?写出解答过程;
(3)连接 , , , .试证明 与 全等;
(4)在(3)的条件下,图中还有哪些其它的全等三角形?请直接写出.
试题篮
()