如图, 是 的直径, 为弦, 的平分线交 于点 ,过点 的切线交 的延长线于点 .
求证:(1) ;
(2) .

如图, 内接于 , 是 的直径.直线 与 相切于点 ,在 上取一点 使得 ,线段 , 的延长线交于点 .
(1)求证:直线 是 的切线;
(2)若 , ,求图中阴影部分的面积(结果保留 .

是
的直径,点
是
上一点,连接
、
,直线
过点
,满足
.

(1)如图①,求证:直线是
的切线;
(2)如图②,点在线段
上,过点
作
于点
,直线
交
于点
、
,连接
并延长交直线
于点
,连接
,且
,若
的半径为1,
,求
的值.
数学课上,张老师举了下面的例题:
例1 等腰三角形 中, ,求 的度数.(答案:
例2 等腰三角形 中, ,求 的度数,(答案: 或 或
张老师启发同学们进行变式,小敏编了如下一题:
变式 等腰三角形 中, ,求 的度数.
(1)请你解答以上的变式题.
(2)解(1)后,小敏发现, 的度数不同,得到 的度数的个数也可能不同,如果在等腰三角形 中,设 ,当 有三个不同的度数时,请你探索 的取值范围.
如图, 内接于 , 是 的直径, 与 相切于点 , 交 的延长线于点 , 为 的中点,连接 .
(1)求证: 是 的切线.
(2)已知 , ,求 , 两点之间的距离.

已知 内接于 , , 的平分线与 交于点 ,与 交于点 ,连接 并延长与 过点 的切线交于点 ,记 .
(1)如图1,若 ,
①直接写出 的值为 ;
②当 的半径为2时,直接写出图中阴影部分的面积为 ;
(2)如图2,若 ,且 , ,求 的长.

问题背景:已知 的顶点 在 的边 所在直线上(不与 , 重合), 交 所在直线于点 , 交 所在直线于点 ,记 的面积为 , 的面积为 .
(1)初步尝试:如图①,当 是等边三角形, , ,且 , 时,则 ;
(2)类比探究:在(1)的条件下,先将点 沿 平移,使 ,再将 绕点 旋转至如图②所示位置,求 的值;
(3)延伸拓展:当 是等腰三角形时,设 .
(Ⅰ)如图③,当点 在线段 上运动时,设 , ,求 的表达式(结果用 , 和 的三角函数表示).
(Ⅱ)如图④,当点 在 的延长线上运动时,设 , ,直接写出 的表达式,不必写出解答过程.

如图,在中,
,
为边
上的点,且
,
为线段
的中点,过点
作
,过点
作
,且
、
相交于点
.
(1)求证:;
(2)求证:.

如图,是
的直径,点
在
的延长线上,
、
是
上的两点,
,
,延长
交
的延长线于点
.
(1)求证:是
的切线;
(2)求证:;
(3)若,
,求弦
的长.

如图, 中, , 的平分线交 于 , 交 的延长线于点 , 交 于点 .
(1)若 ,求 的度数;
(2)若 ,求 的长.
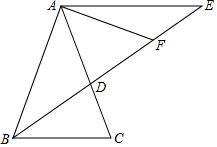
如图, 的外角 的平分线与它的外接圆相交于点 ,连接 , ,过点 作 ,交 于点 .
求证:(1) ;
(2) 为 的切线.

如图,在 中, ,点 在 上.
(1)求作: ,使点 在 上,且 ;(要求:尺规作图,保留作图痕迹,不写作法)
(2)在(1)的条件下,若 .求证: .

试题篮
()