如图,四边形 内接于圆, ,对角线 平分 .
(1)求证: 是等边三角形;
(2)过点 作 交 的延长线于点 ,若 , ,求 的面积.

如图,四边形 为矩形, 是对角线 的中点.连接 并延长至 ,使 ,以 , 为邻边作菱形 ,连接 .
(1)判断四边形 的形状,并证明你的结论.
(2)连接 ,若 ,求 的长.

已知在 中, , 是 边上的一点,将 沿着过点 的直线折叠,使点 落在 边的点 处(不与点 , 重合),折痕交 边于点 .
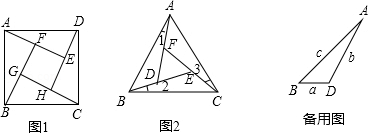
(1)特例感知 如图1,若 , 是 的中点,求证: ;
(2)变式求异 如图2,若 , , ,过点 作 于点 ,求 和 的长;
(3)化归探究 如图3,若 , ,且当 时,存在两次不同的折叠,使点 落在 边上两个不同的位置,请直接写出 的取值范围.

如图1,在平面直角坐标系, 为坐标原点,点 ,点 .
(1)求 的度数;
(2)如图1,将 绕点 顺时针旋转得△ ,当 恰好落在 边上时,设△ 的面积为 ,△ 的面积为 , 与 有何关系?为什么?
(3)若将 绕点 顺时针旋转到如图2所示的位置, 与 的关系发生变化了吗?证明你的判断.

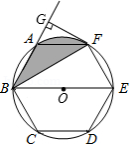
如图,正六边形 内接于 , 是 的直径,连接 ,延长 ,过 作 ,垂足为 .
(1)求证: 是 的切线;
(2)已知 ,求图中阴影部分的面积.
如图,在等边三角形 中,点 是边 上一定点,点 是直线 上一动点,以 为一边作等边三角形 ,连接 .
【问题解决】
如图1,若点 在边 上,求证: ;
【类比探究】
如图2,若点 在边 的延长线上,请探究线段 , 与 之间存在怎样的数量关系?并说明理由.
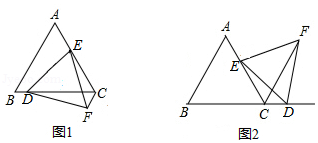
如图1, 是半圆 的直径, 是一条弦, 是 上一点, 于点 ,交 于点 ,连结 交 于点 ,且 .
(1)求证:点 平分 ;
(2)如图2所示,延长 至点 ,使 ,连结 .若点 是线段 的中点.求证: 是 的切线.

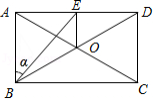
已知:如图,矩形 的对角线 , 相交于点 , , .
(1)求矩形对角线的长;
(2)过 作 于点 ,连结 .记 ,求 的值.
问题背景:如图1,等腰 中, , ,作 于点 ,则 为 的中点, ,于是 ;
迁移应用:如图2, 和 都是等腰三角形, , , , 三点在同一条直线上,连接 .
①求证: ;
②请直接写出线段 , , 之间的等量关系式;
拓展延伸:如图3,在菱形 中, ,在 内作射线 ,作点 关于 的对称点 ,连接 并延长交 于点 ,连接 , .
①证明 是等边三角形;
②若 , ,求 的长.

已知: 在 中, , 为 的中点, , ,垂足分别为点 , ,且 . 求证: 是等边三角形 .

如图,在 中, ,点 , 分别在边 , 上, ,连结 , .
(1)若 ,求 , 的度数;
(2)写出 与 之间的关系,并说明理由.

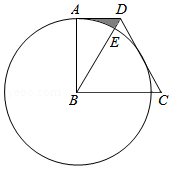
如图,已知 是 的直径,点 是 上一点,连接 ,点 关于 的对称点 恰好落在 上.
(1)求证: ;
(2)过点 作 的切线 ,交 的延长线于点 .如果 , ,求 的直径.

如图,四边形 中, , , ,连接 ,以点 为圆心, 长为半径作 ,交 于点 .
(1)试判断 与 的位置关系,并说明理由;
(2)若 , ,求图中阴影部分的面积.
问题背景
如图1,在正方形 的内部,作 ,根据三角形全等的条件,易得 ,从而得到四边形 是正方形.
类比探究
如图2,在正 的内部,作 , , , 两两相交于 , , 三点 , , 三点不重合)
(1) , , 是否全等?如果是,请选择其中一对进行证明.
(2) 是否为正三角形?请说明理由.
(3)进一步探究发现, 的三边存在一定的等量关系,设 , , ,请探索 , , 满足的等量关系.
试题篮
()