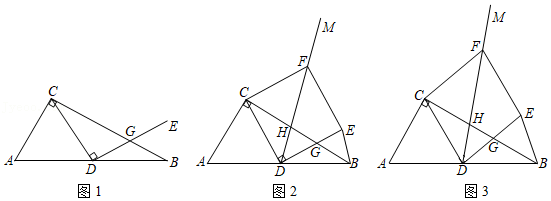
如图①,在 中, , , 是斜边 上的中线,点 为射线 上一点,将 沿 折叠,点 的对应点为点 .

(1)若 .直接写出 的长(用含 的代数式表示);
(2)若 ,垂足为 ,点 与点 在直线 的异侧,连接 ,如②,判断四边形 的形状,并说明理由;
(3)若 ,直接写出 的度数.
如图,在 中, , ,点 为 的中点,连接 ,将线段 绕点 顺时针旋转 得到线段 ,且 交线段 于点 , 的平分线 交 于点 .
(1)如图1,若 ,则线段 与 的数量关系是 , ;
(2)如图2,在(1)的条件下,过点 作 交 于点 ,连接 , .
①试判断四边形 的形状,并说明理由;
②求证: ;
(3)如图3,若 , ,过点 作 交 于点 ,连接 , ,请直接写出 的值(用含 的式子表示).
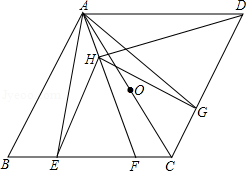
如图,在菱形 中, ,点 , , 分别在边 , 上, , 平分 ,点 是线段 上一动点(与点 不重合).
(1)求证: ;
(2)当 , 时.
求 周长的最小值;
②若点 是 的中点,是否存在直线 将 分成三角形和四边形两部分,其中三角形的面积与四边形的面积比为 .若存在,请求出 的值;若不存在,请说明理由.
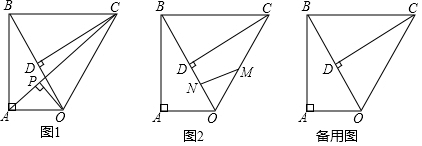
已知Rt△ OAB,∠ OAB=90°,∠ ABO=30°,斜边 OB=4,将Rt△ OAB绕点 O顺时针旋转60°,如图1,连接 BC.
(1)填空:∠ OBC= °;
(2)如图1,连接 AC,作 OP⊥ AC,垂足为 P,求 OP的长度;
(3)如图2,点 M, N同时从点 O出发,在△ OCB边上运动, M沿 O→ C→ B路径匀速运动, N沿 O→ B→ C路径匀速运动,当两点相遇时运动停止,已知点 M的运动速度为1.5单位/秒,点 N的运动速度为1单位/秒,设运动时间为 x秒,△ OMN的面积为 y,求当 x为何值时 y取得最大值?最大值为多少?
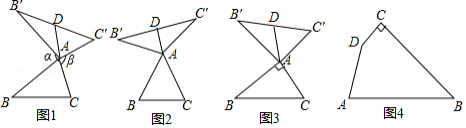
我们定义:如图1,在中,把
绕点
顺时针旋转
得到
,把
绕点
逆时针旋转
得到
,连接
.当
时,我们称△
是
的“旋补三角形”,△
边
上的中线
叫做
的“旋补中线”,点
叫做“旋补中心”.
特例感知:
(1)在图2,图3中,△是
的“旋补三角形”,
是
的“旋补中线”.
①如图2,当为等边三角形时,
与
的数量关系为
;
②如图3,当,
时,则
长为 .
猜想论证:
(2)在图1中,当为任意三角形时,猜想
与
的数量关系,并给予证明.
拓展应用
(3)如图4,在四边形,
,
,
,
,
.在四边形内部是否存在点
,使
是
的“旋补三角形”?若存在,给予证明,并求
的“旋补中线”长;若不存在,说明理由.
试题篮
()