在Rt△ABC中, ,点D为斜边AB的中点, , ,过点A作 且 ,过点E作EF垂直于AC边所在的直线,垂足为点F,连接DF,请你画出图形,并直接写出线段DF的长.
在如图所示的网格中,每个小正方形的边长为1,每个小正方形的顶点叫格点,△ ABC的三个顶点均在格点上,以点 A为圆心的  与 BC相切于点 D,分别交 AB、 AC于点 E、 F.
与 BC相切于点 D,分别交 AB、 AC于点 E、 F.
(1)求△ ABC三边的长;
(2)求图中由线段 EB、 BC、 CF及  所围成的阴影部分的面积.
所围成的阴影部分的面积.

如图,等边△ ABC中, AB=6,点 D在 BC上, BD=4,点 E为边 AC上一动点(不与点 C重合),△ CDE关于 DE的轴对称图形为△ FDE.
(1)当点 F在 AC上时,求证: DF∥ AB;
(2)设△ ACD的面积为 S 1,△ ABF的面积为 S 2,记 S= S 1﹣ S 2, S是否存在最大值?若存在,求出 S的最大值;若不存在,请说明理由;
(3)当 B, F, E三点共线时.求 AE的长.

如图,△ ACE内接于⊙ O, AB是⊙ O的直径,弦 CD⊥ AB于点 H,交 AE于点 F,过点 E作 EG∥ AC,分别交 CD、 AB的延长线于点 G、 M.
(1)求证:△ ECF∽△ GCE;
(2)若tan G= , AH=3 ,求⊙ O半径.

如图,在△ ABC中,∠ BAC=45°, AD⊥ BC于点 D, BD=6, DC=4,求 AD的长.小明同学利用翻折,巧妙地解答了此题,按小明的思路探究并解答下列问题:
(1)分别以 AB, AC所在直线为对称轴,画出△ ABD和△ ACD的对称图形,点 D的对称点分别为点 E, F,延长 EB和 FC相交于点 G,求证:四边形 AEGF是正方形;
(2)设 AD= x,建立关于 x的方程模型,求出 AD的长.
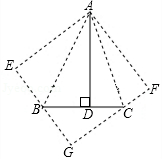
已知,如图,△ ACB和△ ECD都是等腰直角三角形,∠ ACB=∠ ECD=90°, D为 AB边上一点.
(1)求证:△ ACE≌△ BCD;
(2)求证:2 CD 2= AD 2+ DB 2.

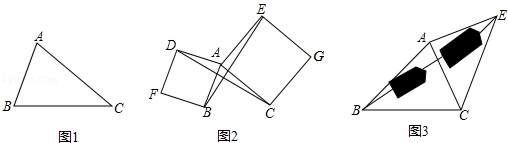
(1)如图1,已知△ABC,以AB、AC为边分别向△ABC外作等边△ABD和等边△ACE,连结BE、CD,请你完成图形(尺规作图,不写作法,保留作图痕迹),并证明:BE=CD;
(2)如图2,已知△ABC,以AB、AC为边分别向外作正方形ABFD和正方形ACGE,连结BE、CD,猜想BE与CD有什么数量关系?并说明理由;
(3)运用(1),(2)解答中所积累的经验和知识,完成下题:
如图(3),要测量池塘两岸相对的两点B、E的距离,已经测得∠ABC=45°,∠CAE=90°,AB=BC=100米,AC=AE,求BE的长(结果保留根号).
如图,在 中,
中, ,
,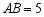 ,
,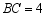 ,将
,将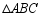 绕点
绕点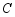 顺时针旋转
顺时针旋转 ,若点
,若点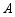 ,
,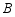 的对应点分别是点
的对应点分别是点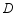 ,
, ,画出旋转后的三角形,并求点
,画出旋转后的三角形,并求点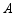 与点
与点 之间的距离.(不要求尺规作图)
之间的距离.(不要求尺规作图)
如图,在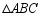 中,
中, ,点
,点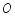 在
在 上,以
上,以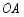 为半径的
为半径的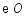 交
交 于点
于点 ,
,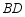 的垂直平分线交
的垂直平分线交 于点
于点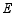 ,交
,交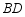 于点
于点 ,连接
,连接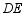 .
.
(1)判断直线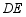 与
与 的位置关系,并说明理由;
的位置关系,并说明理由;
(2)若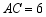 ,
, ,
,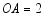 ,求线段
,求线段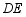 的长.
的长.
图1是某公交公司1路车从起点站 站途经
站途经 站和
站和 站,最终到达终点站
站,最终到达终点站 站的格点站路线图.
站的格点站路线图. 的格点图是由边长为1的小正方形组成)
的格点图是由边长为1的小正方形组成)

(1)求1路车从 站到
站到 站所走的路程(精确到
站所走的路程(精确到 ;
;
(2)在图2、图3和图4的网格中各画出一种从 站到
站到 站的路线图.(要求:①与图1路线不同、路程相同;②途中必须经过两个格点站;③所画路线图不重复)
站的路线图.(要求:①与图1路线不同、路程相同;②途中必须经过两个格点站;③所画路线图不重复)
如图,在△ABC中,∠ABC=90°,以BC为直径作⊙O,交AC于D,E为 的中点,连接CE,BE,BE交AC于F.
(1)求证:AB=AF;
(2)若AB=3,BC=4,求CE的长.

△ABC的顶点坐标为A(﹣2,3)、B(﹣3,1)、C(﹣1,2),以坐标原点O为旋转中心,顺时针旋转90°,得到△A′B′C′,点B′、C′分别是点B、C的对应点.
(1)求过点B′的反比例函数解析式;
(2)求线段CC′的长.

如图,Rt△ ABC中,∠ B=30°,∠ ACB=90°, CD⊥ AB交 AB于 D,以 CD为较短的直角边向△ CDB的同侧作Rt△ DEC,满足∠ E=30°,∠ DCE=90°,再用同样的方法作Rt△ FGC,∠ FCG=90°,继续用同样的方法作Rt△ HIC,∠ HCI=90°.若 AC= a,求 CI的长.

如图, 是 的直径, 是 的一条弦,点 是 上一点,且 , ,与 的延长线交于点 .
(1)求证: 是 的切线;
(2)若 , ,求直径 的长.

试题篮
()