(1)操作发现:如图①,小明画了一个等腰三角形 ,其中 ,在 的外侧分别以 , 为腰作了两个等腰直角三角形 , ,分别取 , , 的中点 , , ,连接 , .小明发现了:线段 与 的数量关系是 ;位置关系是 .
(2)类比思考:
如图②,小明在此基础上进行了深入思考.把等腰三角形 换为一般的锐角三角形,其中 ,其它条件不变,小明发现的上述结论还成立吗?请说明理由.
(3)深入研究:
如图③,小明在(2)的基础上,又作了进一步的探究.向 的内侧分别作等腰直角三角形 , ,其它条件不变,试判断 的形状,并给与证明.

如图, 中, ,以 为直径的 交 于点 ,交 于点 ,过点 作 于点 ,交 的延长线于点 .
(1)求证: 是 的切线;
(2)若 ,求 的值.

如图,点 为 的重心,连接 , 并延长分别交 , 于点 , ,连接 ,若 , , ,则 的长度为

A.1.7B.1.8C.2.2D.2.4
如图,在四边形 中, , ,点 、 分别为 、 的中点,连接 、 、 .
(1)求证: ;
(2)当 时,设 , ,求 , 之间的数量关系式.

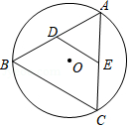
如图,点 、 分别是 的内接正三角形 的 、 边上的中点,若 的半径为2,则 的长等于
A. B. C.1D.
如图,要测定被池塘隔开的 , 两点的距离.可以在 外选一点 ,连接 , ,并分别找出它们的中点 , ,连接 .现测得 , , ,则

A. B. C. D.
如图,三角形纸片 中,点 , , 分别在边 , , 上, , ,将这张纸片沿直线 翻折,点 与点 重合.若 , ,则四边形 的面积为 .
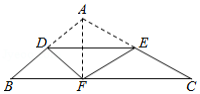
如图,在 中, , 、 分别是 、 的中点,连接 ,过 作 交 的延长线于 .
(1)证明:四边形 是平行四边形;
(2)若四边形 的周长是 , 的长为 ,求线段 的长度.

如图,平行四边形 的对角线 、 相交于点 , 平分 ,分别交 、 于点 、 ,连接 , , ,则下列结论:
① ② ③ ④ ⑤ ,正确的个数是

A.2B.3C.4D.5
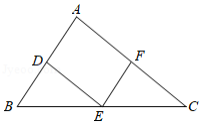
如图,在 中, , , ,点 , , 分别是 , , 的中点,连结 , ,则四边形 的周长为
| A. |
6 |
B. |
9 |
C. |
12 |
D. |
15 |
试题篮
()