如图,将矩形 沿对角线 翻折,点 落在点 处, 交 于 .
(1)求证: ;
(2)若 , ,求图中阴影部分的面积.

如图,矩形 的对角线 , 相交于点 ,点 , 在 上, .
(1)求证: ;
(2)若 , ,求矩形 的面积.

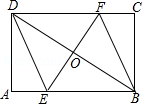
如图,矩形 ABCD中,过对角线 BD中点 O的直线分别交 AB, CD边于点 E、 F.
(1)求证:四边形 BEDF是平行四边形;
(2)只需添加一个条件,即 ,可使四边形 BEDF为菱形.

已知矩形 中, 是 边上的一个动点,点 , , 分别是 , , 的中点.
(1)求证: ;
(2)设 ,当四边形 是正方形时,求矩形 的面积.

如图,四边形 是矩形, , ,以 为一边向矩形外部作等腰直角 , .点 在线段 上,且 ,点 沿折线 运动,点 沿折线 运动(与点 不重合),在运动过程中始终保持线段 .设 与 之间的距离为 .
(1)若 .
①如图1,当点 在线段 上时,若四边形 的面积为48,则 的值为 ;
②在运动过程中,求四边形 的最大面积;
(2)如图2,若点 在线段 上时,要使四边形 的面积始终不小于50,求 的取值范围.

如图,在直角坐标系 中,矩形 的顶点 、 分别在 轴和 轴正半轴上,点 的坐标是 ,点 是 边上一动点(不与点 、点 重合),连接 、 ,过点 作射线 交 的延长线于点 ,交 边于点 ,且 ,令 , .
(1)当 为何值时, ?
(2)求 与 的函数关系式,并写出 的取值范围;
(3)在点 的运动过程中,是否存在 ,使 的面积与 的面积之和等于 的面积?若存在,请求 的值;若不存在,请说明理由.

如图,在矩形 ABCD中, AB=3, BC=5, E是 AD上的一个动点. 
(1)如图1,连接 BD, O是对角线 BD的中点,连接 OE.当 OE= DE时,求 AE的长;
(2)如图2,连接 BE, EC,过点 E作 EF⊥ EC交 AB于点 F,连接 CF,与 BE交于点 G.当 BE平分∠ ABC时,求 BG的长;
(3)如图3,连接 EC,点 H在 CD上,将矩形 ABCD沿直线 EH折叠,折叠后点 D落在 EC上的点 D'处,过点 D′作 D′ N⊥ AD于点 N,与 EH交于点 M,且 AE=1.
①求 的值;
②连接 BE,△ D' MH与△ CBE是否相似?请说明理由.
如图,在矩形 中, , ,点 是 边上的点, ,连接 , 交于点 .
(1)求证: ;
(2)连接 ,求 的值;
(3)连接 交 于点 ,求 的值.

如图,四边形是矩形,
是
边上一点,点
在
的延长线上,且
.
(1)求证:四边形是平行四边形;
(2)连接,若
,
,
,求四边形
的面积.

如图,在矩形 中, ,将 向内翻折,点 落在 上,记为 ,折痕为 .若将 沿 向内翻折,点 恰好落在 上,记为 ,则 .

阅读理解:
我们知道,四边形具有不稳定性,容易变形,如图1,一个矩形发生变形后成为一个平行四边形,设这个平行四边形相邻两个内角中较小的一个内角为α,我们把 的值叫做这个平行四边形的变形度.
(1)若矩形发生变形后的平行四边形有一个内角是120度,则这个平行四边形的变形度是 .
猜想证明:
(2)设矩形的面积为S1,其变形后的平行四边形面积为S2,试猜想S1,S2, 之间的数量关系,并说明理由;
拓展探究:
(3)如图2,在矩形ABCD中,E是AD边上的一点,且 ,这个矩形发生变形后为平行四边形A1B1C1D1,E1为E的对应点,连接B1E1,B1D1,若矩形ABCD的面积为 ,平行四边形A1B1C1D1的面积为 ,试求∠A1E1B1+∠A1D1B1的度数.

如图,矩形ABCD中,AB=6,BC=4,过对角线BD中点O的直线分别交AB,CD边于点E,F.
(1)求证:四边形BEDF是平行四边形;
(2)当四边形BEDF是菱形时,求EF的长.
如图, 为等腰直角三角形,延长 至点 使 , 是矩形,其对角线 , 交于点 ,连接 交 于点 .
(1)求证: ;
(2)求 的值.

试题篮
()