如图,在矩形ABCD中,∠B的平分线BE与AD交于点E,∠BED的平分线EF与DC交于点F,若AB=9,DF=2FC,则BC= .(结果保留根号)

如图(1),菱形ABCD对角线AC、BD的交点O是四边形EFGH对角线FH的中点,四个顶点A、B、C、D分别在四边形EFGH的边EF、FG、GH、HE上.
(1)求证:四边形EFGH是平行四边形;
(2)如图(2)若四边形EFGH是矩形,当AC与FH重合时,已知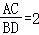 ,且菱形ABCD的面积是20,求矩形EFGH的长与宽.
,且菱形ABCD的面积是20,求矩形EFGH的长与宽.

问题提出:如何将边长为 ,且 为整数)的正方形分割为一些 或 的矩形( 的矩形指边长分别为 , 的矩形)?
问题探究:我们先从简单的问题开始研究解决,再把复杂问题转化为已解决的问题.
探究一:
如图①,当 时,可将正方形分割为五个 的矩形.
如图②,当 时,可将正方形分割为六个 的矩形.
如图③,当 时,可将正方形分割为五个 的矩形和四个 的矩形
如图④,当 时,可将正方形分割为八个 的矩形和四个 的矩形
如图⑤,当 时,可将正方形分割为九个 的矩形和六个 的矩形

探究二:
当 ,11,12,13,14时,分别将正方形按下列方式分割:

所以,当 ,11,12,13,14时,均可将正方形分割为一个 的正方形、一个 的正方形和两个 的矩形.显然, 的正方形和 的矩形均可分割为 的矩形,而 的正方形是边长分别为5,6,7,8,9的正方形,用探究一的方法可分割为一些 或 的矩形.
探究三:
当 ,16,17,18,19时,分别将正方形按下列方式分割:

请按照上面的方法,分别画出边长为18,19的正方形分割示意图.
所以,当 ,16,17,18,19时,均可将正方形分割为一个 的正方形、一个 的正方形和两个 的矩形.显然, 的正方形和 的矩形均可分割为 的矩形,而 的正方形又是边长分别为5,6,7,8,9的正方形,用探究一的方法可分割为一些 或 的矩形.
问题解决:如何将边长为 ,且 为整数)的正方形分割为一些 或 的矩形?请按照上面的方法画出分割示意图,并加以说明.
实际应用:如何将边长为61的正方形分割为一些 或 的矩形?(只需按照探究三的方法画出分割示意图即可)
如图,矩形 中, , , 是 的中点,直线 平行于直线 ,且直线 与直线 之间的距离为2,点 在矩形 边上,将矩形 沿直线 折叠,使点 恰好落在直线 上,则 的长为 .

如图,把一张矩形纸片 沿 折叠后,点 落在 边上的点 处,点 落在点 处,若 ,则图中 的度数为
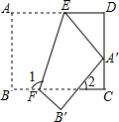
A. B. C. D.
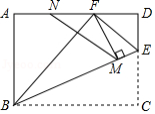
如图,矩形纸片 , , , 为边 上一点.将 沿 所在的直线折叠,点 恰好落在 边上的点 处,过点 作 ,垂足为点 ,取 的中点 ,连接 ,则 .
如图,矩形 中, , ,过点 , 作相距为2的平行线段 , ,分别交 , 于点 , ,则 的长是

A. B. C.1D.
已知四边形 为矩形,延长 到 ,使 ,连接 , 为 的中点,连接 , , 交 于点 ,下列结论:
(1) ;
(2) ;
(3) ;
(4)
其中正确的个数是

A.1B.2C.3D.4
已知四边形 为矩形,延长 到 ,使 ,连接 , 为 的中点,连接 , , 交 于点 ,下列结论:
(1) ;
(2) ;
(3) ;
(4)
其中正确的个数是
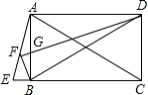
A.1B.2C.3D.4
如图,在矩形 中, , ,点 为线段 上的动点,将 沿 折叠,使点 落在矩形内点 处,下列结论正确的是 (写出所有正确结论的序号)
①当 为线段 中点时, ;
②当 为线段 中点时, ;
③当 、 、 三点共线时, ;
④当 、 、 三点共线时, .

试题篮
()