如图,把某矩形纸片沿
,
折叠(点
,
在
边上,点
,
在
边上),使点
和点
落在
边上同一点
处,
点的对称点为
点,
点的对称点为
点,若
,△
的面积为4,△
的面积为1,则矩形
的面积等于 .

如图,在矩形 中, , ,点 从点 出发,以每秒2个单位长度的速度沿 向点 运动,同时点 从点 出发,以每秒1个单位长度的速度沿 向点 运动,当点 到达点 时,点 , 同时停止运动.连接 , ,设点 运动的时间为 ,若 是以 为底的等腰三角形,则 的值为 .

如图,在平面直角坐标系中,矩形 的顶点 , 分别在 轴、 轴上,对角线 轴,反比例函数 的图象经过矩形对角线的交点 .若点 , ,则 的值为

| A. |
16 |
B. |
20 |
C. |
32 |
D. |
40 |
如图,在平面直角坐标系 中,有一个由六个边长为1的正方形组成的图案,其中点 , 的坐标分别为 , .若过原点的直线 将这个图案分成面积相等的两部分,则直线 的函数解析式为 .
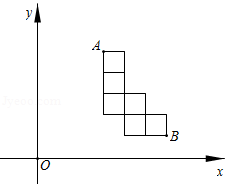
下列命题正确的是
| A. |
A . 平行四边形的对角线互相垂直平分 |
| B. |
B . 矩形的对角线互相垂直平分 |
| C. |
C . 菱形的对角线互相平分且相等 |
| D. |
D . 正方形的对角线互相垂直平分 |
矩形 在平面直角坐标系中的位置如图所示,已知 , ,点 在 轴上,点 在 轴上, 是对角线 上一动点(不与原点重合),连接 ,过点 作 ,交 轴于点 .下列结论:
① ;
②当点 运动到 的中点处时, ;
③在运动过程中, 是一个定值;
④当 为等腰三角形时,点 的坐标为 , .
其中正确结论的个数是

| A. |
1个 |
B. |
2个 |
C. |
3个 |
D. |
4个 |
综合与实践
背景阅读 早在三千多年前,我国周朝数学家商高就提出:将一根直尺折成一个直角,如果勾等于三,股等于四,那么弦就等于五,即“勾三、股四、弦五”.它被记载于我国古代著名数学著作《周髀算经》中,为了方便,在本题中,我们把三边的比为的三角形称为
,4,
型三角形,例如:三边长分别为9,12,15或
,
,
的三角形就是
,4,
型三角形,用矩形纸片按下面的操作方法可以折出这种类型的三角形.
实践操作 如图1,在矩形纸片中,
,
.
第一步:如图2,将图1中的矩形纸片沿过点
的直线折叠,使点
落在
上的点
处,折痕为
,再沿
折叠,然后把纸片展平.
第二步:如图3,将图2中的矩形纸片再次折叠,使点与点
重合,折痕为
,然后展平,隐去
.
第三步:如图4,将图3中的矩形纸片沿折叠,得到△
,再沿
折叠,折痕为
,
与折痕
交于点
,然后展平.

问题解决
(1)请在图2中证明四边形是正方形.
(2)请在图4中判断与
的数量关系,并加以证明;
(3)请在图4中证明,4,
型三角形;
探索发现
(4)在不添加字母的情况下,图4中还有哪些三角形是,4,
型三角形?请找出并直接写出它们的名称.
综合与实践
问题情境:在数学活动课上,老师出示了这样一个问题:如图1,在矩形中,
,
是
延长线上一点,且
,连接
,交
于点
,以
为一边在
的左下方作正方形
,连接
.试判断线段
与
的位置关系.
探究展示:勤奋小组发现,垂直平分
,并展示了如下的证明方法:
证明:,
.
,
.
四边形
是矩形,
.
.(依据
,
.
.
即是
的
边上的中线,
又,
.(依据
垂直平分
.
反思交流:
(1)①上述证明过程中的“依据1”“依据2”分别是指什么?
②试判断图1中的点是否在线段
的垂直平分线上,请直接回答,不必证明;
(2)创新小组受到勤奋小组的启发,继续进行探究,如图2,连接,以
为一边在
的左下方作正方形
,发现点
在线段
的垂直平分线上,请你给出证明;
探索发现:
(3)如图3,连接,以
为一边在
的右上方作正方形
,可以发现点
,点
都在线段
的垂直平分线上,除此之外,请观察矩形
和正方形
的顶点与边,你还能发现哪个顶点在哪条边的垂直平分线上,请写出一个你发现的结论,并加以证明.

在平面直角坐标系中,四边形是矩形,点
,点
,点
.以点
为中心,顺时针旋转矩形
,得到矩形
,点
,
,
的对应点分别为
,
,
.
(Ⅰ)如图①,当点落在
边上时,求点
的坐标;
(Ⅱ)如图②,当点落在线段
上时,
与
交于点
.
①求证;
②求点的坐标.
(Ⅲ)记为矩形
对角线的交点,
为
的面积,求
的取值范围(直接写出结果即可).

如图,矩形 中, , ,双曲线 的图象分别交 , 于点 , ,连接 , , , ,则 值为

A. B.1C. D.
试题篮
()