初中数学圆内接四边形的性质试题

如图，△ABC中，点O是边AC上一个动点，过O作直线MN∥BC．设MN交∠ACB的平分线于点E，交∠ACB的外角平分线于点F．

（1）求证：OE=OF；
（2）若CE=8，CF=6，求OC的长；
（3）当点O在边AC上运动到什么位置时，四边形AECF是矩形？并说明理由．

如图1，四边形 $\mathit{ABCD}$ 内接于 $\odot O$ ， $\mathit{AD}$ 为直径，点 $C$ 作 $\mathit{CE}\perp \mathit{AB}$ 于点 $E$ ，连接 $\mathit{AC}$ ．

（1）求证： $\angle \mathit{CAD}=\angle \mathit{ECB}$ ；

（2）若 $\mathit{CE}$ 是 $\odot O$ 的切线， $\angle \mathit{CAD}=30°$ ，连接 $\mathit{OC}$ ，如图2．

①请判断四边形 $\mathit{ABCO}$ 的形状，并说明理由；

②当 $\mathit{AB}=2$ 时，求 $\mathit{AD}$ ， $\mathit{AC}$ 与 $\stackrel{̂}{\mathit{CD}}$ 围成阴影部分的面积．

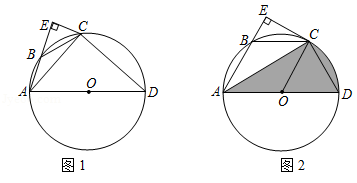
如图所示，在直角梯形ABCD中，AD//BC，∠A＝90°，AB＝12，BC＝21，AD=16。动点P从点B出发，沿射线BC的方向以每秒2个单位长的速度运动，动点Q同时从点A出发，在线段AD上以每秒1个单位长的速度向点D运动，当其中一个动点到达端点时另一个动点也随之停止运动。设运动的时间为t（秒）。

（1）设△DPQ的面积为S，用含有t的代数式表示S。
（2）当t为何值时，四边形PCDQ是平行四边形？

（1）如图1，将直角的顶点E放在正方形ABCD的对角线AC上，使角的一边交CD于点F，另一边交CB或其延长线于点G，求证：EF=EG；
（2）如图2，将（1）中的“正方形ABCD”改成“矩形ABCD”，其他条件不变．若AB=m，BC=n，试求的值；
（3）如图3，将直角顶点E放在矩形ABCD的对角线交点，EF、EG分别交CD与CB于点F、G，且EC平分∠FEG．若AB=2，BC=4，求EG、EF的长．

动手实验：利用矩形纸片（图1）剪出一个正六边形纸片；利用这个正六边形纸片做一个如图（2）无盖的正六棱柱（棱柱底面为正六边形）；
（1）做一个这样的正六棱柱所需最小的矩形纸片的长与宽的比为多少？
（2）在（1）的前提下，当矩形的长为2时，要使无盖正六棱柱侧面积最大，正六棱柱的高为多少？并求此时矩形纸片的利用率？（矩形纸片的利用率=无盖正六棱柱的表面积/矩形纸片的面积）

（本题共7分）如果一个点与另外两个点能构成直角三角形，则称这个点为另外两个点的勾股点．例如：矩形ABCD中，点C与A、B两点可构成直角三角形ABC，则称点C为A、B两点的勾股点，同样，点D也是A、B两点的勾股点．
（1）如图1，矩形ABCD中，AB =2，BC =1，请在边CD上作出A、B两点的勾股点（点C和点D除外）．（要求：尺规作图，保留作图痕迹，不要求写作法）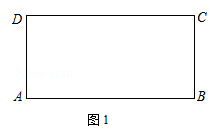

（2）如图2，矩形ABCD中，若AB =3，BC =1，点P在边CD上（点C和点D除外），且点P为A、B两点的勾股点，求DP的长．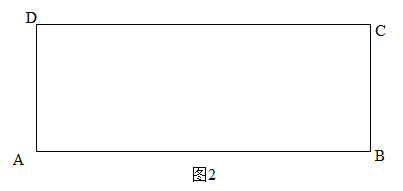

如图，分别以直角△ABC的斜边AB，直角边AC为边向△ABC外作等边△ABD和等边△ACE，F为AB的中点，DE与AB交于点G，EF与AC交于点H，∠ACB=90°，∠BAC=30°．给出如下结论：
①EF⊥AC；②四边形ADFE为菱形；③AD=4AG；④FH=BD；其中正确结论的是（   ）

A．①②③

B．①②④

C．①③④

D．②③④

如图，在△ABC中，AB=6，BC=9,AC=8，点P在△ABC内部，过点P分别画AB、BC、CA的平行线，与各边分别相交得线段DE、FG、HK，已知线段DE、FG、HK的长度都为d,求d的值．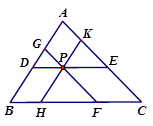

在 $\mathit{\Delta ABC}$ 中， $\angle \mathit{ACB}=90°$ ，分别过点 $B$ ， $C$ 作 $\angle \mathit{BAC}$ 平分线的垂线，垂足分别为点 $D$ ， $E$ ， $\mathit{BC}$ 的中点是 $M$ ，连接 $\mathit{CD}$ ， $\mathit{MD}$ ， $\mathit{ME}$ ．则下列结论错误的是 $($ 　　 $)$

A．

$\mathit{CD}=2\mathit{ME}$

B．

$\mathit{ME}//\mathit{AB}$

C．

$\mathit{BD}=\mathit{CD}$

D．

$\mathit{ME}=\mathit{MD}$

如图，在锐角三角形 $\mathit{ABC}$中， $\mathit{AD}$是 $\mathit{BC}$边上的高，以 $\mathit{AD}$为直径的 $\odot O$交 $\mathit{AB}$于点 $E$，交 $\mathit{AC}$于点 $F$，过点 $F$作 $\mathit{FG}\perp \mathit{AB}$，垂足为 $H$，交 $\stackrel{̂}{\mathit{AE}}$于点 $G$，交 $\mathit{AD}$于点 $M$，连接 $\mathit{AG}$， $\mathit{DE}$， $\mathit{DF}$．

（1）求证： $\angle \mathit{GAD}+\angle \mathit{EDF}=180°$；

（2）若 $\angle \mathit{ACB}=45°$， $\mathit{AD}=4$， $\tan \angle \mathit{ABC}=2$，求 $\mathit{HF}$的长．

如图．在边长为6的正方形 $\mathit{ABCD}$中，点 $E$， $F$分别在 $\mathit{BC}$， $\mathit{CD}$上， $\mathit{BC}=3\mathit{BE}$且 $\mathit{BE}=\mathit{CF}$， $\mathit{AE}\perp \mathit{BF}$，垂足为 $G$， $O$是对角线 $\mathit{BD}$的中点，连接 $\mathit{OG}$、则 $\mathit{OG}$的长为 　　．

已知矩形长和宽分别为4和2，是否存在另一个矩形，它的周长和面积分别是已知矩形的？若存在请计算这个矩形的两边长，若不存在请说明理由．

如图所示，已知△ABC中，AC=BC=6，∠C=90°．O是AB的中点，⊙O与AC相切于点D、与BC相切于点E．设⊙O交OB于F，连DF并延长交CB的延长线于G．

（1）∠BFG与∠BGF是否相等?为什么?
（2）求由DG、GE和所围成的图形的面积（阴影部分）．

如图，周长为16的菱形ABCD中，点E，F分别在AB，AD边上，AE=1，AF=3，P为BD上一动点，则线段EP+FP的长最短为（   ）

A．3

B．4

C．5

D．6

已知菱形ABCD边长为5cm，tan∠DAB=,连接AC、BD,过点B作BE⊥AB分别交AC、CD于E、F。若点P为AD上一点，且∠DPE+∠DAB=90⁰,则AP长为          ．