初中数学圆内接四边形的性质解答题

我县城区青印溪两岸堤坝的横截面是如图所示的梯形ABCD，背水坡AD的坡度i（即tanα）为1:1.2，坝高为5m，现为响应上级“搞好民生水利工程”的号召，决定加固堤坝。要求坝顶CD加宽lm，形成新的背水坡EF，其坡度为1:1.4，已知堤坝总长度为3000m
完成该工程需要多少土方?
该工程由甲、乙两个工程队同时合作完成，按原计划需要20天．准备开工前接到上级通知，汛期可能提前，要求两个工程队提高工作效率，甲队工作效率提高30％，乙队工作效率提高40％，结果提前5天完成．问这两个工程队原计划每天各完成多少土方?

如图，四边形ABCD为矩形，AB＝4，AD＝3，动点M、N分别从D、B同时出发，以1个单位/秒的速度运动，点M沿DA向终点A运动，点N沿BC向终点C运动。过点N作NP⊥BC，交AC于点P，连结MP。已知动点运动了秒。

请直接写出PN的长           ；（用含的代数式表示）
若0秒≤≤3秒，试求△MPA的面积S与时间秒的函数关系式，并求S的最大值。
若0秒≤≤3秒，△MPA能否与△PCN相似？若能，试求出相似时的对应值；若不能，试说明理由。

计算 ．
画出函数y=-x²+1的图象
已知：如图，E，F分别是□ABCD的边AD，BC的中点．求证：AF=CE．

如图，在梯形中，，对角线平分，的平分线交于分别是的中点．
求证：
当与满足怎样的数量关系时，？并说明理由．

如图，正方形ABCD，点E、F分别为BC、CD边上的点，连接EF，点 M为EF上一点，且使AE平分∠BAM，AF平分∠DAF, 证明：∠EAF=45°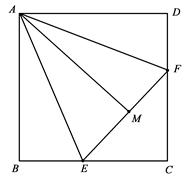

在8×8正方形网格中建立如图的平面直角坐标系，己知A（2，4），B（4，2）．
C是第一象限内一个格点，由点C与线段AB组成一个以AB为底，且腰长为无理数的等腰三角形.
填空：C点的坐标是_________，△ABC的面积是__________；
将△ABC绕点C旋转180°得到△A₁B₁C，连结AB₁，BA₁，试判断四边形AB₁A₁B是何种特殊四边形，请说明理由；
请探究：在x轴上是否存在这样的点P，使四边形ABOP的面积等于△ABC面积
2倍．若存在，请直接写出点P的坐标（不必写出解答过程）；若不存在，请说明理由．

已知：如图，在等腰梯形ABCD中，AD∥BC，AB＝DC，点E为边BC上一点，且AE＝DC。

求证：四边形AECD是平行四边形
当等腰梯形ABCD满足__  ▲ 时（添加一个条件），
则四边形AECD是菱形。

如图：△ABC中，AD是边BC上的中线，过点A作AE∥BC，过点D作DE∥AB与AC、AE分别交于点O、E，连接EC.

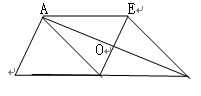
求证：AD=EC；
当∠BAC=90º时,求证:四边形ADCE是菱形；
在(2)的条件下,若AB=AO,且OD=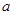,求菱形ADCE的周长.

如图，在□ABCD的对角线AC 上取两点E和F，若AE=CF.
求证：∠AFD=∠CEB.

如图，E、F，是平行四边形ABCD的对角线AC上的两点，AF=CE连接D,E,F和F,B.求证：四边形DFBE是平行四边形。
 

如图，在梯形中，两点在边上，且四边形是平行四边形．

与有何等量关系？请说明理由
当时，求证：四边形是矩形

已知：如图，在平行四边形ABCD中，E、F分别是AD、BC的中点，求证：BE=DF

在□ABCD中，∠BAD的平分线交直线BC于点E，交直线DC于点F。
在图1中证明
若，G是EF的中点（如图2），直接写出∠BDG的度数；
若，FG∥CE，，分别连结DB、DG（如图3），求∠BDG的度数。

已知: 如图, 在□ABCD中,  E、F是对角线AC上的两点, 且AE = CF.
求证: 四边形BFDE是平行四边形

如图，在梯形ABCD中，AD//BC，E是BC的中点，AD=5，BC=12，CD=，∠C=45°，点P是BC边上一动点，设PB的长为x．
当x的值为____________时，以点P、A、D、E为顶点的四边形为直角梯形
当x的值为____________时，以点P、A、D、E为顶点的四边形为平行四边形；
点P在BC边上运动的过程中，以P、A、D、E为顶点的四边形能否构成菱形？试说明理由．