初中数学圆内接四边形的性质解答题

已知：如图，点E、F分别为□ABCD 的BC、AD边上的点，且∠1="∠2." 求证：AE="FC."

已知：如图，在中，E、F、G、H分别是AB、BC、CD、DA上的点，且AE=CG，BF=DH．求证：≌．

如图，已知四边形ABCD的对角线AC、BD相交于点O，△ABC≌△BAD．

求证：OA=OB；
若∠CAB=35°，求∠CDB的度数．

如图，在□ABCD中，E、F为BC两点，且BE＝CF，AF＝DE．求证：
△ABF≌△DCE；
四边形ABCD是矩形

如图，在□ABCD中，BE平分∠ABC交AD于点E，DF平分∠ADC交BC于点F．

△ABE≌△CDF
若BD⊥EF，则判断四边形EBFD是什么特殊四边形，请证明你的结论．

在下面所给的图形中，若连接BC，则四边形ABCD是矩形，四边形CBEF是平行四边形。用铅笔和三角板画图：

在图1中画出两条线段，将整个图形分成面积相等的两个部分（不写画法）；
在图2中画出一条线段，还能够将整个图形分成面积相等的两个部分，并写出画法的主要步骤。

在2ABCD中，对角线BD、AC相交于点O，BE=DF，过点O作线段GH交AD于点G，交BC于点H，顺次连接EH、HF、FG、GE，求证：四边形EHFG是平行四边形。

如图，已知点D在△ABC的BC边上，DE∥AC交AB于E，DF∥AB交AC于F．
求证：AE=DF；
若AD平分∠BAC，试判断四边形AEDF的形状，并说明理由．

你能找出两种不同方法把一个正方形划分为9个小正方形吗？

在数学活动课上，小明提出这样一个问题：∠B=∠C=90°，E是BC的中点，DE 平分∠ADC，∠CED=35°，如图，则∠EAB是             ．

如图，AC是平行四边形ABCD的对角线，∠ACB=∠ACD.

求证：AB=AD

已知，如图，Ｅ、Ｆ分别为矩形ＡＢＣＤ的边ＡＤ和ＢＣ上的点，ＡＥ＝ＣＦ．

求证：ＢＥ＝ＤＦ．

如图：E、F分别是 中AD、BC边上的点，AE=CF，

(1)求证：四边形BEDF是平行四边形；
(2)若M、N分别是BE、DF的中点，连结MF、EN、EF，当EF与BC具有怎样的位置关系时，四边形EMFN是菱形，并证明你的结论。

如图，梯形ABCD中，AD∥BC，BA＝AD＝DC，点E在CB延长线上，BE＝AD，连接AC、AE．（1）求证：AE＝AC（2）若AB⊥AC， F是BC的中点，试判断四边形AFCD的形状，并说明理由．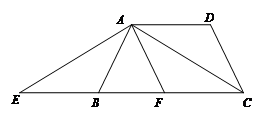

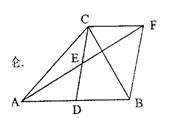
如图，在△ABC中，D是AB的中点，E是CD的中点，过点C作CF∥AB交AE的延长线于点F，连结BF。
求证：△ADE≌△FCE；
若AC=BC，试判断四边形BDCF的形状，并证明你的结论。