如图,点 是 的边 上一点,以 为半径的 与边 相切于点 ,与边 , 分别相交于点 , ,且 .
(1)求证: ;
(2)当 , 时,求 的长.
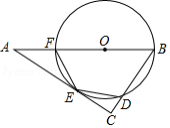
如图,点 在 外, 是 的切线, 为切点,直线 与 相交于点 、 .
(1)若 ,求证: ;
(2)小明发现, 在一定范围内变化时,始终有 成立.请你写出推理过程.

如图,已知 是 的直径,点 是 上一点,连接 ,点 关于 的对称点 恰好落在 上.
(1)求证: ;
(2)过点 作 的切线 ,交 的延长线于点 .如果 , ,求 的直径.

如图,AB是半圆O的直径,点P是BA延长线上一点,PC是⊙O的切线,切点为C,过点B作BD⊥PC交PC的延长线于点D,连接BC.求证:
(1)∠PBC=∠CBD;
(2)BC2=AB•BD.
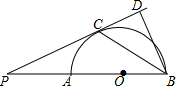
如图,已知 为半圆 的直径, 为半圆 上一点,连接 , ,过点 作 于点 ,过点 作半圆 的切线交 的延长线于点 ,连接 并延长交 于点 .
(1)求证: ;
(2)若半圆 的直径为10, ,求 的长.

如图, 为 的内接三角形, 为 的直径,过点 作 的切线交 的延长线于点 .
(1)求证: ;
(2)过点 作 的切线 交 于点 ,求证: ;
(3)若点 为直径 下方半圆的中点,连接 交 于点 ,且 , ,求 的长.
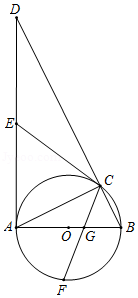
如图,在Rt△ABC中, ,点O在AB上,经过点A的⊙O与BC相切于点D,与AC,AB分别相交于点E,F,连接AD与EF相交于点G.
(1)求证:AD平分∠CAB;
(2)若 于点H,FH平分 .
①试判断DF与DH的数量关系,并说明理由;
②求⊙O的半径.

如图,点 A, B, C, D是直径为 AB的⊙ O上的四个点, C是劣弧 的中点, AC与 BD交于点 E.
(1)求证: DC 2= CE• AC;
(2)若 AE=2, EC=1,求证:△ AOD是正三角形;
(3)在(2)的条件下,过点 C作⊙ O的切线,交 AB的延长线于点 H,求△ ACH的面积.
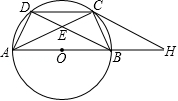
如图,在 中, , , (圆心 在 内部)经过 、 两点,交 于点 ,过点 作 的切线交 于点 .延长 交 于点 ,作 交 于点
(1)求证:四边形 是平行四边形;
(2)若 , ,求 的值.
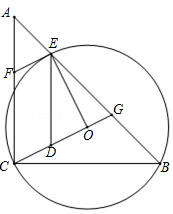
如图, 是 的直径, ,四边形 是平行四边形, 交 于点 ,连接 并延长交 的延长线于点 .
(1)求证: 是 的切线;
(2)若 , ,求图中阴影部分的面积(结果保留根号和 ).
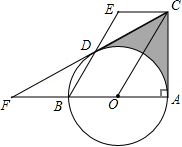
如图, 是 的外接圆,直线 与 相切于点 , ,连接 交 于点 .
(1)求证: 平分 ;
(2)若 的平分线 交 于点 ,且 , ,求 的长.
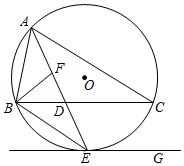
如图,已知⊙ O的半径为2, AB为直径, CD为弦. AB与 CD交于点 M,将 沿 CD翻折后,点 A与圆心 O重合,延长 OA至 P,使 AP= OA,连接 PC
(1)求 CD的长;
(2)求证: PC是⊙ O的切线;
(3)点 G为 的中点,在 PC延长线上有一动点 Q,连接 QG交 AB于点 E.交 于点 F( F与 B、 C不重合).问 GE• GF是否为定值?如果是,求出该定值;如果不是,请说明理由.

如图,在△ ABC中, AB= AC,以 AC为直径作⊙ O交 BC与 D点,过点 D作⊙ O的切线 EF,交 AB于点 E,交 AC的延长线于点 F.
(1)求证: FE⊥ AB.
(2)当 AE=6, AF=10时,求 BE的长.

如图,四边形 ABCD中, MA= MC, MB= MD,以 AB为直径的圆 O过点 M且与 DC延长线相切于点 E.
(1)求证:四边形 ABCD是菱形;
(2)若 AB=4,求 的长(结果请保留π)

试题篮
()