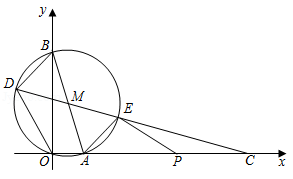
如图,在平面直角坐标系中, 经过原点 ,分别交 轴、 轴于点 , ,连结 .直线 分别交 于点 , (点 在左侧),交 轴于点 ,连结 .
(1)求 的半径和直线 的函数表达式;
(2)求点 , 的坐标;
(3)点 在线段 上,连结 .当 与 的一个内角相等时,求所有满足条件的 的长.
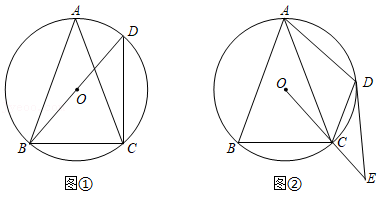
已知 内接于 , , ,点 是 上一点.
(Ⅰ)如图①,若 为 的直径,连接 ,求 和 的大小;
(Ⅱ)如图②,若 ,连接 ,过点作 的切线,与 的延长线交于点 ,求 的大小.
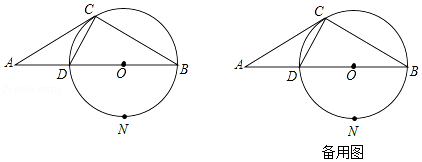
如图, 的半径为1,点 是 的直径 延长线上的一点, 为 上的一点, , .
(1)求证:直线 是 的切线;
(2)求 的面积;
(3)点 在 上运动(不与 、 重合),过点 作 的垂线,与 的延长线交于点 .
①当点 运动到与点 关于直径 对称时,求 的长;
②当点 运动到什么位置时, 取到最大值,并求出此时 的长.
如图, 是 的直径, 为 上一点 不与点 , 重合)连接 , ,过点 作 ,垂足为点 .将 沿 翻折,点 落在点 处得 , 交 于点 .
(1)求证: 是 的切线;
(2)若 , ,求阴影部分面积.
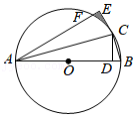
如图,在 中, 为 的直径, 为 的弦,点 是 的中点,过点 作 的垂线,交 于点 ,交 于点 ,分别连接 , .
(1) 与 的数量关系是 ;
(2)求证: ;
(3)若 , ,求阴影部分图形的面积.

定义:三角形一个内角的平分线和与另一个内角相邻的外角平分线相交所成的锐角称为该三角形第三个内角的遥望角.
(1)如图1, 是 中 的遥望角,若 ,请用含 的代数式表示 .
(2)如图2,四边形 内接于 , ,四边形 的外角平分线 交 于点 ,连结 并延长交 的延长线于点 .求证: 是 中 的遥望角.
(3)如图3,在(2)的条件下,连结 , ,若 是 的直径.
①求 的度数;
②若 , ,求 的面积.

问题提出
(1)如图1,在 中, , , 的平分线交 于点 .过点 分别作 , .垂足分别为 , ,则图1中与线段 相等的线段是 .
问题探究
(2)如图2, 是半圆 的直径, . 是 上一点,且 ,连接 , . 的平分线交 于点 ,过点 分别作 , ,垂足分别为 , ,求线段 的长.
问题解决
(3)如图3,是某公园内“少儿活动中心”的设计示意图.已知 的直径 ,点 在 上,且 . 为 上一点,连接 并延长,交 于点 .连接 , .过点 分别作 , ,垂足分别为 , .按设计要求,四边形 内部为室内活动区,阴影部分是户外活动区,圆内其余部分为绿化区.设 的长为 ,阴影部分的面积为 .
①求 与 之间的函数关系式;
②按照“少儿活动中心”的设计要求,发现当 的长度为 时,整体布局比较合理.试求当 时.室内活动区(四边形 的面积.

如图1, 是 的直径 上的一点,过 作 交 于 、 , 是 上的一点,过 的直线分别与 、 的延长线相交于 、 ,连接 交 于 , .
(1)求证: 是 的切线;
(2)若 , 的半径为4, ,求 的长;
(3)如图2,在(2)的条件下,连接 、 ;在线段 上有一点 ,并且以 、 、 为顶点的三角形与 相似,求 的长度.

已知平面图形 ,点 、 是 上任意两点,我们把线段 的长度的最大值称为平面图形 的“宽距”.例如,正方形的宽距等于它的对角线的长度.
(1)写出下列图形的宽距:
①半径为1的圆: ;
②如图1,上方是半径为1的半圆,下方是正方形的三条边的“窗户形“: ;
(2)如图2,在平面直角坐标系中,已知点 、 , 是坐标平面内的点,连接 、 、 所形成的图形为 ,记 的宽距为 .
①若 ,用直尺和圆规画出点 所在的区域并求它的面积(所在区域用阴影表示);
②若点 在 上运动, 的半径为1,圆心 在过点 且与 轴垂直的直线上.对于 上任意点 ,都有 ,直接写出圆心 的横坐标 的取值范围.

如图①,在平面直角坐标系中,圆心为 的动圆经过点 且与 轴相切于点 .
(1)当 时,求 的半径;
(2)求 关于 的函数解析式,请判断此函数图象的形状,并在图②中画出此函数的图象;
(3)请类比圆的定义(圆可以看成是到定点的距离等于定长的所有点的集合),给(2)中所得函数图象进行定义:此函数图象可以看成是到 的距离等于到 的距离的所有点的集合.
(4)当 的半径为1时,若 与以上(2)中所得函数图象相交于点 、 ,其中交点 在点 的右侧,请利用图②,求 的大小.

如图,菱形 中,对角线 , 相交于点 , , ,动点 从点 出发,沿线段 以 的速度向点 运动,同时动点 从点 出发,沿线段 以 的速度向点 运动,当其中一个动点停止运动时另一个动点也随之停止.设运动时间为 ,以点 为圆心, 长为半径的 与射线 ,线段 分别交于点 , ,连接 .
(1)求 的长(用含有 的代数式表示),并求出 的取值范围;
(2)当 为何值时,线段 与 相切?
(3)若 与线段 只有一个公共点,求 的取值范围.

已知四边形 是 的内接四边形, 是 的直径, ,垂足为 .
(1)延长 交 于点 ,延长 , 交于点 ,如图1.求证: ;
(2)过点 作 ,垂足为 , 交 于点 ,且点 和点 都在 的左侧,如图2.若 , , ,求 的大小.

如果三角形三边的长 、 、 满足 ,那么我们就把这样的三角形叫做“匀称三角形”,如:三边长分别为1,1,1或3,5,7, 的三角形都是“匀称三角形”.
(1)如图1,已知两条线段的长分别为 、 .用直尺和圆规作一个最短边、最长边的长分别为 、 的“匀称三角形”(不写作法,保留作图痕迹);
(2)如图2, 中, ,以 为直径的 交 于点 ,过点 作 的切线交 延长线于点 ,交 于点 ,若 ,判断 是否为“匀称三角形”?请说明理由.

如图,在 中, ,点 在 上,以 为直径的 与边 相切于点 ,与边 相交于点 ,且 ,连接 并延长交 于点 ,连接 .
(1)求证:
① .
② 是 的切线.
(2)若 ,求图形中阴影部分的面积.

试题篮
()