如图,已知 为 的角平分线, , ,以 为圆心, 为半径的圆分别交 , 于点 , ,连接 并延长交 于点 .
(1)求证: 是 的切线;
(2)求 的值;
(3)求 的值.

如图, 是 的直径,弦 ,垂足为 ,连接 ,过 上一点 作 交 的延长线于点 ,连接 交 于点 ,且 ,连接 .
(1)求证: ;
(2)求证: 是 的切线;
(3)延长 交 的延长线于点 ,若 , ,求 的值.

如图所示, 是 的直径,点 是 延长线上的一点,过点 作 的切线,切点为 ,连接 , .
(1)求证: .
(2)若点 在 的延长线上运动, 的平分线交 于点 ,你认为 的大小是否发生变化?若变化,请说明理由;若没有变化,求出 的大小.
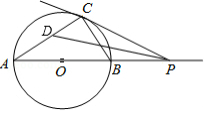
如图,点 是 的边 上一点,以 为半径的 与边 相切于点 ,与边 , 分别相交于点 , ,且 .
(1)求证: ;
(2)当 , 时,求 的长.
如图,在 中, 为直角, , ,半径为2的动圆圆心 从点 出发,沿着 方向以1个单位长度 秒的速度匀速运动,同时动点 从点 出发,沿着 方向也以1个单位长度 秒的速度匀速运动,设运动时间为 秒 以 为圆心, 长为半径的 与 、 的另一个交点分别为 、 ,连接 、 .
(1)当 为何值时,点 与点 重合?
(2)当 经过点 时,求 被 截得的弦长.
(3)若 与线段 只有一个公共点,求 的取值范围.
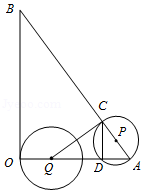
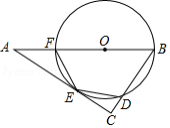
如图,已知四边形 内接于 , 是 的中点, 于 ,与 及 的延长线交于点 、 ,且 .
(1)求证: ;
(2)如果 , ,求 的值.

如图,已知 的半径为 ,射线 经过点 , ,射线 与 相切于点 . 、 两点同时从点 出发,点 以 的速度沿射线 方向运动,点 以 的速度沿射线 方向运动,设运动时间为 .
(1)求 的长;
(2)当直线 与 相切时,求证: ;
(3)当 为何值时,直线 与 相切?

如图,在 中, ,以 为半径作 ,交 于点 ,交 的延长线于点 ,连接 , .
(1)求证: ;
(2)当 时,求 ;
(3)在(2)的条件下,作 的平分线,与 交于点 ,若 ,求 的半径.

如图,在 中, ,以 为直径的 与边 , 分别交于 , 两点,过点 作 于点 .
(1)判断 与 的位置关系,并说明理由;
(2)求证: 为 的中点;
(3)若 , ,求 的长.

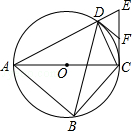
如图,四边形ABCD内接于⊙O,对角线AC为⊙O的直径,过点C作AC的垂线交AD的延长线于点E,点F为CE的中点,连接DB,DC,DF.
(1)求 的度数;
(2)求证:DF是⊙O的切线;
(3)若 ,求 的值.
数学活动﹣旋转变换
(1)如图①,在△ABC中, ,将△ABC绕点C逆时针旋转50°得到△A′B′C,连接BB′,求∠A′B′B的大小;
(2)如图②,在△ABC中, , , ,将△ABC绕点C逆时针旋转60°得到△A′B′C,连接BB′,以A′为圆心,A′B′长为半径作圆.
(Ⅰ)猜想:直线BB′与⊙A′的位置关系,并证明你的结论;
(Ⅱ)连接A′B,求线段A′B的长度;
(3)如图③,在△ABC中, , , ,将△ABC绕点C逆时针旋转2β角度 得到△A′B′C,连接A′B和BB′,以A′为圆心,A′B′长为半径作圆,问:角α与角β满足什么条件时,直线BB′与⊙A′相切,请说明理由,并求此条件下线段A′B的长度(结果用角α或角β的三角函数及字母m、n所组成的式子表示)

如图所示,在Rt△ABC与Rt△OCD中, ,O为AB的中点.
(1)求证: .
(2)已知点E在AB上,且 .
(i)若 , ,求CE的长;
(ii)试判定CD与以A为圆心、AE为半径的⊙A的位置关系,并请说明理由.
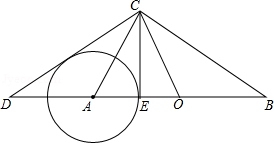
在平面直角坐标系中,△ABC三个顶点坐标为 、 、
(1)求△ABC内切圆⊙D的半径.
(2)过点 的直线与⊙D相切于点F(点F在第一象限),求直线EF的解析式.
(3)以(2)为条件,P为直线EF上一点,以P为圆心,以 为半径作⊙P.若⊙P上存在一点到△ABC三个顶点的距离相等,求此时圆心P的坐标.
如图,在Rt△ ABC中,∠ C=90°,以 BC为直径的⊙ O交斜边 AB于点 M,若 H是 AC的中点,连接 MH.
(1)求证: MH为⊙ O的切线.
(2)若 ,求⊙ O的半径.
(3)在(2)的条件下分别过点 A、 B作⊙ O的切线,两切线交于点 D, AD与⊙ O相切于 N点,过 N点作 NQ⊥ BC,垂足为 E,且交⊙ O于 Q点,求线段 NQ的长度.

试题篮
()