初中数学圆的综合题解答题

如图，AB为△ABC外接圆⊙O的直径，点P是线段CA延长线上一点，点E在圆上且满足PE²＝PA•PC，连接CE，AE，OE，OE交CA于点D．

（1）求证：△PAE∽△PEC；

（2）求证：PE为⊙O的切线；

（3）若∠B＝30°， $\mathit{AP}=\frac{1}{2}\mathit{AC}$，求证：DO＝DP．

如图，在△ABC中，∠C＝90°，∠BAC的平分线交BC于点D，DE⊥AD，交AB于点E，AE为⊙O的直径

（1）判断BC与⊙O的位置关系，并证明你的结论；

（2）求证：△ABD∽△DBE；

（3）若 $=\cos B=\frac{2\sqrt{2}}{3}$，AE＝4，求CD．

如图，在四边形ABCD中，AB＝6，BC＝8，CD＝24，AD＝26，∠B＝90°，以AD为直径作圆O，过点D作DE∥AB交圆O于点E

（1）证明点C在圆O上；

（2）求tan∠CDE的值；

（3）求圆心O到弦ED的距离．

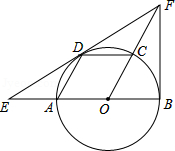
如图，AB是⊙O的直径，点C、D在圆上，且四边形AOCD是平行四边形，过点D作⊙O的切线，分别交OA延长线与OC延长线于点E、F，连接BF．

（1）求证：BF是⊙O的切线；

（2）已知圆的半径为1，求EF的长．

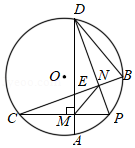
如图，已知⊙ O的半径为2， AB为直径， CD为弦． AB与 CD交于点 M，将 $\stackrel{̂}{\mathit{CD}}$ 沿 CD翻折后，点 A与圆心 O重合，延长 OA至 P，使 AP＝ OA，连接 PC

（1）求 CD的长；

（2）求证： PC是⊙ O的切线；

（3）点 G为 $\stackrel{̂}{\mathit{ADB}}$ 的中点，在 PC延长线上有一动点 Q，连接 QG交 AB于点 E．交 $\stackrel{̂}{\mathit{BC}}$ 于点 F（ F与 B、 C不重合）．问 GE• GF是否为定值？如果是，求出该定值；如果不是，请说明理由．

我们知道，顶点坐标为 $(h,k)$ 的抛物线的解析式为 $y=a{(x-h)}^2+k(a\ne 0)$ ．今后我们还会学到，圆心坐标为 $(a,b)$ ，半径为 $r$ 的圆的方程 ${(x-a)}^2+{(y-b)}^2=r^2$ ，如：圆心为 $P(-2,1)$ ，半径为3的圆的方程为 ${(x+2)}^2+{(y-1)}^2=9$ ．

（1）以 $M(-3,-1)$ 为圆心， $\sqrt{3}$ 为半径的圆的方程为 　 　．

（2）如图，以 $B(-3,0)$ 为圆心的圆与 $y$ 轴相切于原点， $C$ 是 $\odot B$ 上一点，连接 $\mathit{OC}$ ，作 $\mathit{BD}\perp \mathit{OC}$ ，垂足为 $D$ ，延长 $\mathit{BD}$ 交 $y$ 轴于点 $E$ ，已知 $\sin \angle \mathit{AOC}=\frac{3}{5}$ ．

①连接 $\mathit{EC}$ ，证明： $\mathit{EC}$ 是 $\odot B$ 的切线；

②在 $\mathit{BE}$ 上是否存在一点 $Q$ ，使 $\mathit{QB}=\mathit{QC}=\mathit{QE}=\mathit{QO}$ ？若存在，求点 $Q$ 的坐标，并写出以 $Q$ 为圆心，以 $\mathit{QB}$ 为半径的 $\odot Q$ 的方程；若不存在，请说明理由．

如图， $\mathit{BC}$ 是 $\odot O$ 的直径， $\mathit{AD}$ 是 $\odot O$ 的弦， $\mathit{AD}$ 交 $\mathit{BC}$ 于点 $E$ ，连接 $\mathit{AB}$ ， $\mathit{CD}$ ，过点 $E$ 作 $\mathit{EF}\perp \mathit{AB}$ ，垂足为 $F$ ， $\angle \mathit{AEF}=\angle D$ ．

（1）求证： $\mathit{AD}\perp \mathit{BC}$ ；

（2）点 $G$ 在 $\mathit{BC}$ 的延长线上，连接 $\mathit{AG}$ ， $\angle \mathit{DAG}=2\angle D$ ．

①求证： $\mathit{AG}$ 与 $\odot O$ 相切；

②当 $\frac{\mathit{AF}}{\mathit{BF}}=\frac{2}{5}$ ， $\mathit{CE}=4$ 时，直接写出 $\mathit{CG}$ 的长．

如图，在 $\odot O$ 中，点 $P$ 为 $\stackrel{̂}{\mathit{AB}}$ 的中点，弦 $\mathit{AD}$ 、 $\mathit{PC}$ 互相垂直，垂足为 $M$ ， $\mathit{BC}$ 分别与 $\mathit{AD}$ 、 $\mathit{PD}$ 相交于点 $E$ 、 $N$ ，连接 $\mathit{BD}$ 、 $\mathit{MN}$ ．

（1）求证： $N$ 为 $\mathit{BE}$ 的中点．

（2）若 $\odot O$ 的半径为8， $\stackrel{̂}{\mathit{AB}}$ 的度数为 $90°$ ，求线段 $\mathit{MN}$ 的长．

如图1，与直线相离，过圆心作直线的垂线，垂足为，且交于、两点在、之间）．我们把点称为关于直线的“远点“，把的值称为关于直线的“特征数”．

（1）如图2，在平面直角坐标系中，点的坐标为．半径为1的与两坐标轴交于点、、、．

①过点画垂直于轴的直线，则关于直线的“远点”是点　　（填“”．“ ”、“ ”或“” ，关于直线的“特征数”为　　；

②若直线的函数表达式为．求关于直线的“特征数”；

（2）在平面直角坐标系中，直线经过点，点是坐标平面内一点，以为圆心，为半径作．若与直线相离，点是关于直线的“远点”．且关于直线的“特征数”是，求直线的函数表达式．

定义：对角线互相垂直且相等的四边形叫做垂等四边形．

（1）下面四边形是垂等四边形的是 　 　；（填序号）

①平行四边形；②矩形；③菱形；④正方形

（2）图形判定：如图1，在四边形 $\mathit{ABCD}$ 中， $\mathit{AD}//\mathit{BC}$ ， $\mathit{AC}\perp \mathit{BD}$ ，过点 $D$ 作 $\mathit{BD}$ 垂线交 $\mathit{BC}$ 的延长线于点 $E$ ，且 $\angle \mathit{DBC}=45°$ ，证明：四边形 $\mathit{ABCD}$ 是垂等四边形．

（3）由菱形面积公式易知性质：垂等四边形的面积等于两条对角线乘积的一半．应用：在图2中，面积为24的垂等四边形 $\mathit{ABCD}$ 内接于 $\odot O$ 中， $\angle \mathit{BCD}=60°$ ．求 $\odot O$ 的半径．

定义：有一组对角互余的四边形叫做对余四边形．

理解：

（1）若四边形 $\mathit{ABCD}$ 是对余四边形，则 $\angle A$ 与 $\angle C$ 的度数之和为 　     　；

证明：

（2）如图1， $\mathit{MN}$ 是 $\odot O$ 的直径，点 $A$ ， $B$ ， $C$ 在 $\odot O$ 上， $\mathit{AM}$ ， $\mathit{CN}$ 相交于点 $D$ ．

求证：四边形 $\mathit{ABCD}$ 是对余四边形；

探究：

（3）如图2，在对余四边形 $\mathit{ABCD}$ 中， $\mathit{AB}=\mathit{BC}$ ， $\angle \mathit{ABC}=60°$ ，探究线段 $\mathit{AD}$ ， $\mathit{CD}$ 和 $\mathit{BD}$ 之间有怎样的数量关系？写出猜想，并说明理由．

如图，在 $\text{Rt}\Delta \text{ABC}$ 中， $\angle C=90°$ ， $\mathit{AD}$ 平分 $\angle \mathit{BAC}$ 交 $\mathit{BC}$ 于点 $D$ ， $O$ 为 $\mathit{AB}$ 上一点，经过点 $A$ 、 $D$ 的 $\odot O$ 分别交 $\mathit{AB}$ 、 $\mathit{AC}$ 于点 $E$ 、 $F$ ．

（1）求证： $\mathit{BC}$ 是 $\odot O$ 的切线；

（2）若 $\mathit{BE}=8$ ， $\sin B=\frac{5}{13}$ ，求 $\odot O$ 的半径；

（3）求证： $A{D}^2=\mathit{AB}·\mathit{AF}$ ．

如图所示：与的边相切于点，与、分别交于点、，．是的直径．连接，过作交于，连接、，与交于点．

（1）求证：直线与相切；

（2）求证：；

（3）若，时，过作交于、两点在线段上），求的长．

如图，在中，以为直径的交于点，连接，且，连接并延长交的延长线于点，与相切于点．

（1）求证：是的切线；

（2）连接交于点，求证：；

（3）若，求的值．

如图， $\odot O$ 为等边 $\mathit{\Delta ABC}$ 的外接圆，半径为2，点 $D$ 在劣弧 $\stackrel{̂}{\mathit{AB}}$ 上运动（不与点 $A$ ， $B$ 重合），连接 $\mathit{DA}$ ， $\mathit{DB}$ ， $\mathit{DC}$ ．

（1）求证： $\mathit{DC}$ 是 $\angle \mathit{ADB}$ 的平分线；

（2）四边形 $\mathit{ADBC}$ 的面积 $S$ 是线段 $\mathit{DC}$ 的长 $x$ 的函数吗？如果是，求出函数解析式；如果不是，请说明理由；

（3）若点 $M$ ， $N$ 分别在线段 $\mathit{CA}$ ， $\mathit{CB}$ 上运动（不含端点），经过探究发现，点 $D$ 运动到每一个确定的位置， $\mathit{\Delta DMN}$ 的周长有最小值 $t$ ，随着点 $D$ 的运动， $t$ 的值会发生变化，求所有 $t$ 值中的最大值．