初中数学圆的综合题解答题

已知：在矩形中，，分别是边，上的点，过点作的垂线交于点，以为直径作半圆．

（1）填空：点　　（填“在”或“不在” 上；当时，的值是　　；

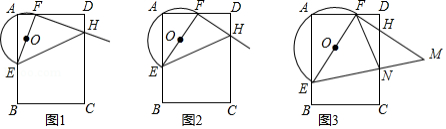
（2）如图1，在中，当时，求证：；

（3）如图2，当的顶点是边的中点时，求证：；

（4）如图3，点在线段的延长线上，若，连接交于点，连接，当时，，，求的值．

已知内接于，的平分线交于点，连接，．

（1）如图①，当时，请直接写出线段，，之间满足的等量关系式：　　；

（2）如图②，当时，试探究线段，，之间满足的等量关系，并证明你的结论；

（3）如图③，若，，求的值．

如图，在中，是斜边的中点，以为直径作圆交于点，延长至，使，连接、，交圆于点．

（1）判断四边形的形状，并说明理由；

（2）求证：；

（3）若，，求的长．

如图，内接于，，是的直径，与相交于点，过点作，分别交、的延长线于点、，连接．

（1）求证：是的切线；

（2）求证：．

如图1，已知外一点向作切线，点为切点，连接并延长交于点，连接并延长交于点，过点作，分别交于点，交于点，连接．

（1）求证：；

（2）如图2，当时

①求的度数；

②连接，在上是否存在点使得四边形是菱形．若存在，请直接写出的值；若不存在，请说明理由．

如图，在中，，的平分线交于点，点在上，以为直径的经过点．

（1）求证：①是的切线；

②；

（2）若点是劣弧的中点，且，试求阴影部分的面积．

如图，已知是的直径，，为圆上一点，且，连接，，，与交于点．

（1）求证：为的切线；

（2）若，求的值．

如图，是的直径，点是延长线上一点，过点作的切线，切点是，过点作弦于，连接，．

（1）求证：是的切线；

（2）若，，求的长；

（3）试探究线段，，之间的数量关系，并说明理由．

如图，是的直径，点为上一点，于点，交于点，点为的延长线上一点，的延长线与的延长线交于点，且，连结、、．

（1）求证：为的切线；

（2）过作于点，求证：；

（3）如果，，求的长．

如图，在菱形中，连结、交于点，过点作于点，以点为圆心，为半径的半圆交于点．

①求证：是的切线．

②若且，求图中阴影部分的面积．

③在②的条件下，是线段上的一动点，当为何值时，的值最小，并求出最小值．

已知在平面直角坐标系中，直线分别交轴和轴于点，．

（1）如图1，已知经过点，且与直线相切于点，求的直径长；

（2）如图2，已知直线分别交轴和轴于点和点，点是直线上的一个动点，以为圆心，为半径画圆．

①当点与点重合时，求证：直线与相切；

②设与直线相交于，两点，连结，．问：是否存在这样的点，使得是等腰直角三角形，若存在，求出点的坐标；若不存在，请说明理由．

如图，是的直径，切于点，交于点，平分，连接．

（1） 求证：；

（2） 若，，求的半径 ．

已知是的直径，是的切线，，交于点，是上一点，延长交于点．

（1）如图①，求和的大小；

（2）如图②，当时，求的大小．

阅读以下材料，并按要求完成相应的任务：

莱昂哈德欧拉是瑞士数学家，在数学上经常见到以他的名字命名的重要常数，公式和定理，下面就是欧拉发现的一个定理：在中，和分别为外接圆和内切圆的半径，和分别为其中外心和内心，则．

如图1，和分别是的外接圆和内切圆，与相切分于点，设的半径为，的半径为，外心（三角形三边垂直平分线的交点）与内心（三角形三条角平分线的交点）之间的距离，则有．

下面是该定理的证明过程（部分）

延长交于点，过点作的直径，连接，．

，（同弧所对的圆周角相等）．

．，，①

如图2，在图1（隐去，的基础上作的直径，连接，，，．

是的直径，所以．

与相切于点，所以，

．

（同弧所对的圆周角相等），

，

．

②

任务：（1）观察发现：，　　（用含，的代数式表示）；

（2）请判断和的数量关系，并说明理由．

（3）请观察式子①和式子②，并利用任务（1），（2）的结论，按照上面的证明思路，完成该定理证明的剩余部分；

（4）应用：若的外接圆的半径为，内切圆的半径为，则的外心与内心之间的距离为　　．

如图1，的直径，是弦上一动点（与点，不重合），，过点作交于点．

（1）如图2，当时，求的长；

（2）如图3，当时，延长至点，使，连接．

①求证：是的切线；

②求的长．