如图①,半圆O的直径AB=6,AM和BN是它的两条切线,CP与半圆O相切于点P,并于AM,BN分别相交于C,D两点.
(1)请直接写出∠COD的度数;
(2)求AC•BD的值;
(3)如图②,连接OP并延长交AM于点Q,连接DQ,试判断△PQD能否与△ACO相似?若能相似,请求AC:BD的值;若不能相似,请说明理由.

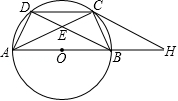
如图,点 A, B, C, D是直径为 AB的⊙ O上的四个点, C是劣弧 的中点, AC与 BD交于点 E.
(1)求证: DC 2= CE• AC;
(2)若 AE=2, EC=1,求证:△ AOD是正三角形;
(3)在(2)的条件下,过点 C作⊙ O的切线,交 AB的延长线于点 H,求△ ACH的面积.
如图,在△ ABC中,∠ C=90°, D、 F是 AB边上两点,以 DF为直径的⊙ O与 BC相交于点 E,连接 EF,∠ OFE= ∠ A.过点 F作 FG⊥ BC于点 G,交⊙ O于点 H,连接 EH.
(1)求证: BC是⊙ O的切线;
(2)连接 ED,过点 E作 EQ⊥ AB,垂足为 Q,△ EQD和△ EGH全等吗?若全等,请予以证明;若不全等,请说明理由;
(3)当 BO=5, BE=4时,求△ EHG的面积.

如图,在△ABC中,∠C=90°,D、F是AB边上两点,以DF为直径的⊙O与BC相交于点E,连接EF,∠OFE= ∠A.过点F作FG⊥BC于点G,交⊙O于点H,连接EH.
(1)求证:BC是⊙O的切线;
(2)连接ED,过点E作EQ⊥AB,垂足为Q,△EQD和△EGH全等吗?若全等,请予以证明;若不全等,请说明理由;
(3)当BO=5,BE=4时,求△EHG的面积.

在平面直角坐标系中,已知点 A(﹣2,0), B(2,0), C(3,5).
(1)求过点 A, C的直线解析式和过点 A, B, C的抛物线的解析式;
(2)求过点 A, B及抛物线的顶点 D的⊙ P的圆心 P的坐标;
(3)在抛物线上是否存在点 Q,使 AQ与⊙ P相切,若存在请求出 Q点坐标.

如图,在平面直角坐标系中, O(0,0), A(0,﹣6), B(8,0)三点在⊙ P上, M为劣弧的 中点.
(1)求圆的半径及圆心 P的坐标;
(2)求证: AM是∠ OAB的平分线;
(3)连接 BM并延长交 y轴于点 N,求 N, M点的坐标.

如图,在△ABC中,AB=AC,点D在BC上,BD=DC,过点D作DE⊥AC,垂足为E,⊙O经过A,B,D三点.
(1)求证:AB是⊙O的直径;
(2)判断DE与⊙O的位置关系,并加以证明;
(3)若⊙O的半径为3,∠BAC=60°,求DE的长.

已知 是
是 的直径,点
的直径,点 在
在 上,点
上,点 在半径
在半径 上(不与点
上(不与点 ,
, 重合).
重合).
(1)如图1,若 ,
, ,求
,求 的度数.
的度数.
(2)如图2,点 在线段
在线段 上(不与
上(不与 ,
, 重合),
重合), 、
、 的延长线分别交
的延长线分别交 于点
于点 、
、 ,连接
,连接 ,
, ,点
,点 是
是 的延长线与
的延长线与 的交点,若
的交点,若 ,
, ,
, ,
, ,求
,求 的长.
的长.

我们知道:垂直于弦的直径平分这条弦,并且平分这条弦所对的两条弧;平分弧的直径垂直平分这条弧所对的弦.你可以利用这一结论解决问题:
如图,点 在以
在以 (南北方向)为直径的
(南北方向)为直径的 上,
上, ,
, 交
交 于点
于点 ,垂足为
,垂足为 ,
, ,弦
,弦 、
、 分别交
分别交 于点
于点 、
、 ,且
,且 .
.
(1)比较 与 的大小;
(2)若 ,求证:
,求证: ;
;
(3)设直线 、
、 相交所成的锐角为
相交所成的锐角为 ,试确定
,试确定 时,点
时,点 的位置.
的位置.

如图,线段 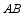 是
是 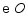 的直径,弦
的直径,弦 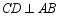 于点
于点 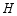 ,点
,点 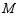 是
是 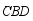 上任意一点,
上任意一点, 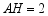 ,
, 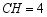 .
.
(1)求 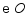 的半径
的半径 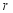 的长度;
的长度;
(2)求 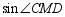 ;
;
(3)直线 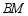 交直线
交直线 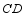 于点
于点 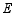 ,直线
,直线 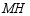 交
交 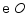 于点
于点 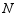 ,连接
,连接 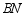 交
交 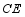 于点
于点 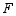 ,求
,求 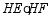 的值.
的值.
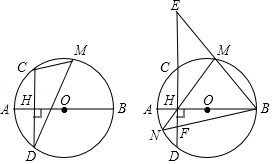
如图,AB为△ABC外接圆⊙O的直径,点P是线段CA延长线上一点,点E在圆上且满足PE2=PA•PC,连接CE,AE,OE,OE交CA于点D.
(1)求证:△PAE∽△PEC;
(2)求证:PE为⊙O的切线;
(3)若∠B=30°, ,求证:DO=DP.

如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,DE⊥AD,交AB于点E,AE为⊙O的直径
(1)判断BC与⊙O的位置关系,并证明你的结论;
(2)求证:△ABD∽△DBE;
(3)若 ,AE=4,求CD.

如图,在四边形ABCD中,AB=6,BC=8,CD=24,AD=26,∠B=90°,以AD为直径作圆O,过点D作DE∥AB交圆O于点E
(1)证明点C在圆O上;
(2)求tan∠CDE的值;
(3)求圆心O到弦ED的距离.

如图,AB是⊙O的直径,点C、D在圆上,且四边形AOCD是平行四边形,过点D作⊙O的切线,分别交OA延长线与OC延长线于点E、F,连接BF.
(1)求证:BF是⊙O的切线;
(2)已知圆的半径为1,求EF的长.
试题篮
()