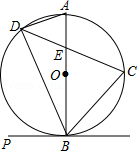
如图, 、 是以 为直径的 上的点, ,弦 交 于点 .
(1)当 是 的切线时,求证: ;
(2)求证: ;
(3)已知 , 是半径 的中点,求线段 的长.
已知:如图, 是 的直径, ,点 , 是 上两点,连接 , , ,弦 平分 , ,过点 作 交 的延长线于点 ,垂足为点 .
(1)求扇形 的面积(结果保留 ;
(2)求证: 是 的切线.

如图,动点 在以 为圆心, 为直径的半圆弧上运动(点 不与点 、 及 的中点 重合),连接 .过点 作 于点 ,以 为边在半圆同侧作正方形 ,过点 作 的切线交射线 于点 ,连接 、 .
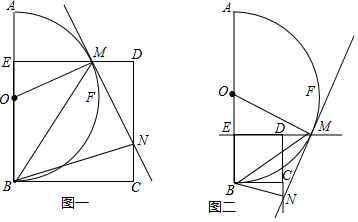
(1)探究:如图一,当动点 在 上运动时;
①判断 是否成立?请说明理由;
②设 , 是否为定值?若是,求出该定值,若不是,请说明理由;
③设 , 是否为定值?若是,求出该定值,若不是,请说明理由;
(2)拓展:如图二,当动点 在 上运动时;
分别判断(1)中的三个结论是否保持不变?如有变化,请直接写出正确的结论.(均不必说明理由)
如图,在 中, ,以 为直径的 交 于点 , 是 的中点, 交 于点 .
(1)若 , ,求 的长;
(2)判断直线 与 的位置关系,并说明理由;
(3)求证: .

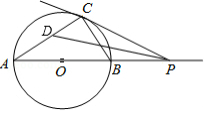
如图,点 是 直径 延长线上的一点, 在 上, ,
(1)求证: 是 的切线;
(2)若 的半径为2,求 的面积.

(2) , ,
,
;
又 ,
,
;
方法一:在 中, ,
连接 ,设 的半径为 ,则在 中, ,即
解得:
方法二: ,过点 作 于点 ,则
在 中,

本题考查了圆的综合题:圆的切线垂直于过切点的半径;利用勾股定理计算线段的长.
如图,四边形 内接于圆 , , 为直径,过点 作圆 的切线交 的延长线于点 ,过 的三等分点 (靠近点 作 的平行线交 于点 ,连接 .
(1)求证: ;
(2)求证: ;
(3)当 , 时,求 的长.
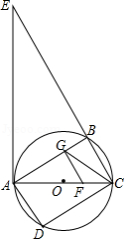
如图, 是以 为直径的 的切线, 为切点, 平分 ,弦 交 于点 , .
(1)求证: 是等腰直角三角形;
(2)求证: ;
(3)求 的值.

如图,已知 为 的角平分线, , ,以 为圆心, 为半径的圆分别交 , 于点 , ,连接 并延长交 于点 .
(1)求证: 是 的切线;
(2)求 的值;
(3)求 的值.

如图, 是 的直径,弦 ,垂足为 ,连接 ,过 上一点 作 交 的延长线于点 ,连接 交 于点 ,且 ,连接 .
(1)求证: ;
(2)求证: 是 的切线;
(3)延长 交 的延长线于点 ,若 , ,求 的值.

如图所示, 是 的直径,点 是 延长线上的一点,过点 作 的切线,切点为 ,连接 , .
(1)求证: .
(2)若点 在 的延长线上运动, 的平分线交 于点 ,你认为 的大小是否发生变化?若变化,请说明理由;若没有变化,求出 的大小.
如图,点 是 的边 上一点,以 为半径的 与边 相切于点 ,与边 , 分别相交于点 , ,且 .
(1)求证: ;
(2)当 , 时,求 的长.
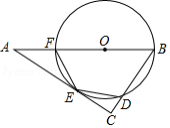
如图,在 中, 为直角, , ,半径为2的动圆圆心 从点 出发,沿着 方向以1个单位长度 秒的速度匀速运动,同时动点 从点 出发,沿着 方向也以1个单位长度 秒的速度匀速运动,设运动时间为 秒 以 为圆心, 长为半径的 与 、 的另一个交点分别为 、 ,连接 、 .
(1)当 为何值时,点 与点 重合?
(2)当 经过点 时,求 被 截得的弦长.
(3)若 与线段 只有一个公共点,求 的取值范围.
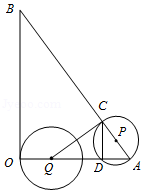
如图,已知四边形 内接于 , 是 的中点, 于 ,与 及 的延长线交于点 、 ,且 .
(1)求证: ;
(2)如果 , ,求 的值.

试题篮
()