初中数学圆的综合题解答题

如图，△ ABC内接于⊙ O， BC＝2， AB＝ AC，点 D为 $\stackrel{⏜}{\mathit{AC}}$ 上的动点，且cos∠ ABC＝ $\frac{\sqrt{10}}{10}$ ．

（1）求 AB的长度；

（2）在点 D的运动过程中，弦 AD的延长线交 BC延长线于点 E，问 AD• AE的值是否变化？若不变，请求出 AD• AE的值；若变化，请说明理由；

（3）在点 D的运动过程中，过 A点作 AH⊥ BD，求证： BH＝ CD+ DH．

如图，是所对弦上一动点，过点作交于点，连接，过点作于点．已知，设、两点间的距离为，、两点间的距离为．（当点与点或点重合时，的值为

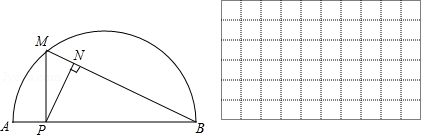
小东根据学习函数的经验，对函数随自变量的变化而变化的规律进行了探究．

下面是小东的探究过程，请补充完整：

（1）通过取点、画图、测量，得到了与的几组值，如下表：

	0	1	2	3	4	5	6
	0	2.0	2.3	2.1		0.9	0

（说明：补全表格时相关数值保留一位小数）

（2）建立平面直角坐标系，描出已补全后的表中各对对应值为坐标的点，画出该函数的图象．

（3）结合画出的函数图象，解决问题：当为等腰三角形时，的长度约为　　．

如图，是的直径，点是延长线上一点，过点作的切线，切点是，过点作弦于，连接，．

（1）求证：是的切线；

（2）若，，求的长；

（3）试探究线段，，之间的数量关系，并说明理由．

如图，以Rt△ ABC的直角边 AB为直径的⊙ O交斜边 AC于点 D，过点 D作⊙ O的切线与 BC交于点 E，弦 DM与 AB垂直，垂足为 H．

（1）求证： E为 BC的中点；

（2）若⊙ O的面积为12π，两个三角形△ AHD和△ BMH的外接圆面积之比为3，求△ DEC的内切圆面积 S ₁和四边形 OBED的外接圆面积 S ₂的比．

如图，在菱形中，连结、交于点，过点作于点，以点为圆心，为半径的半圆交于点．

①求证：是的切线．

②若且，求图中阴影部分的面积．

③在②的条件下，是线段上的一动点，当为何值时，的值最小，并求出最小值．

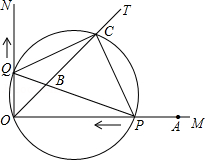
如图，点在数轴上对应的数为26，以原点为圆心，为半径作优弧，使点在右下方，且，在优弧上任取一点，且能过作直线交数轴于点，设在数轴上对应的数为，连接．

（1）若优弧上一段的长为，求的度数及的值；

（2）求的最小值，并指出此时直线与所在圆的位置关系；

（3）若线段的长为12.5，直接写出这时的值．

如图1，的直径，是弦上一动点（与点，不重合），，过点作交于点．

（1）如图2，当时，求的长；

（2）如图3，当时，延长至点，使，连接．

①求证：是的切线；

②求的长．

阅读以下材料，并按要求完成相应的任务：

莱昂哈德欧拉是瑞士数学家，在数学上经常见到以他的名字命名的重要常数，公式和定理，下面就是欧拉发现的一个定理：在中，和分别为外接圆和内切圆的半径，和分别为其中外心和内心，则．

如图1，和分别是的外接圆和内切圆，与相切分于点，设的半径为，的半径为，外心（三角形三边垂直平分线的交点）与内心（三角形三条角平分线的交点）之间的距离，则有．

下面是该定理的证明过程（部分）

延长交于点，过点作的直径，连接，．

，（同弧所对的圆周角相等）．

．，，①

如图2，在图1（隐去，的基础上作的直径，连接，，，．

是的直径，所以．

与相切于点，所以，

．

（同弧所对的圆周角相等），

，

．

②

任务：（1）观察发现：，　　（用含，的代数式表示）；

（2）请判断和的数量关系，并说明理由．

（3）请观察式子①和式子②，并利用任务（1），（2）的结论，按照上面的证明思路，完成该定理证明的剩余部分；

（4）应用：若的外接圆的半径为，内切圆的半径为，则的外心与内心之间的距离为　　．

如图，点 $P$为正方形 $\mathit{ABCD}$的对角线 $\mathit{AC}$上的一点，连接 $\mathit{BP}$并延长交 $\mathit{CD}$于点 $E$，交 $\mathit{AD}$的延长线于点 $F$， $\odot O$是 $\mathit{\Delta DEF}$的外接圆，连接 $\mathit{DP}$．

（1）求证： $\mathit{DP}$是 $\odot O$的切线；

（2）若 $\tan \angle \mathit{PDC}=\frac{1}{2}$，正方形 $\mathit{ABCD}$的边长为4，求 $\odot O$的半径和线段 $\mathit{OP}$的长．

我们知道，顶点坐标为 $(h,k)$ 的抛物线的解析式为 $y=a{(x-h)}^2+k(a\ne 0)$ ．今后我们还会学到，圆心坐标为 $(a,b)$ ，半径为 $r$ 的圆的方程 ${(x-a)}^2+{(y-b)}^2=r^2$ ，如：圆心为 $P(-2,1)$ ，半径为3的圆的方程为 ${(x+2)}^2+{(y-1)}^2=9$ ．

（1）以 $M(-3,-1)$ 为圆心， $\sqrt{3}$ 为半径的圆的方程为 　 　．

（2）如图，以 $B(-3,0)$ 为圆心的圆与 $y$ 轴相切于原点， $C$ 是 $\odot B$ 上一点，连接 $\mathit{OC}$ ，作 $\mathit{BD}\perp \mathit{OC}$ ，垂足为 $D$ ，延长 $\mathit{BD}$ 交 $y$ 轴于点 $E$ ，已知 $\sin \angle \mathit{AOC}=\frac{3}{5}$ ．

①连接 $\mathit{EC}$ ，证明： $\mathit{EC}$ 是 $\odot B$ 的切线；

②在 $\mathit{BE}$ 上是否存在一点 $Q$ ，使 $\mathit{QB}=\mathit{QC}=\mathit{QE}=\mathit{QO}$ ？若存在，求点 $Q$ 的坐标，并写出以 $Q$ 为圆心，以 $\mathit{QB}$ 为半径的 $\odot Q$ 的方程；若不存在，请说明理由．

如图，已知 $\angle \mathit{MON}=90°$ ， $\mathit{OT}$ 是 $\angle \mathit{MON}$ 的平分线， $A$ 是射线 $\mathit{OM}$ 上一点， $\mathit{OA}=8\mathit{cm}$ ．动点 $P$ 从点 $A$ 出发，以 $1\mathit{cm}/s$ 的速度沿 $\mathit{AO}$ 水平向左作匀速运动，与此同时，动点 $Q$ 从点 $O$ 出发，也以 $1\mathit{cm}/s$ 的速度沿 $\mathit{ON}$ 竖直向上作匀速运动．连接 $\mathit{PQ}$ ，交 $\mathit{OT}$ 于点 $B$ ．经过 $O$ 、 $P$ 、 $Q$ 三点作圆，交 $\mathit{OT}$ 于点 $C$ ，连接 $\mathit{PC}$ 、 $\mathit{QC}$ ．设运动时间为 $t\left(s\right)$ ，其中 $0<t<8$ ．

（1）求 $\mathit{OP}+\mathit{OQ}$ 的值；

（2）是否存在实数 $t$ ，使得线段 $\mathit{OB}$ 的长度最大？若存在，求出 $t$ 的值；若不存在，说明理由．

（3）求四边形 $\mathit{OPCQ}$ 的面积．

（1）如图1，点为矩形对角线上一点，过点作，分别交、于点、．若，，的面积为，的面积为，则　 　；

（2）如图2，点为内一点（点不在上），点、、、分别为各边的中点．设四边形的面积为，四边形的面积为（其中，求的面积（用含、的代数式表示）；

（3）如图3，点为内一点（点不在上），过点作，，与各边分别相交于点、、、．设四边形的面积为，四边形的面积为（其中，求的面积（用含、的代数式表示）；

（4）如图4，点、、、把四等分．请你在圆内选一点（点不在、上），设、、围成的封闭图形的面积为，、、围成的封闭图形的面积为，的面积为，的面积为，根据你选的点的位置，直接写出一个含有、、、的等式（写出一种情况即可）．

如图，半径为4的中，弦的长度为，点是劣弧上的一个动点，点是弦的中点，点是弦的中点，连接、、．

（1）求的度数；

（2）当点沿着劣弧从点开始，逆时针运动到点时，求的外心所经过的路径的长度；

（3）分别记，的面积为，，当时，求弦的长度．

如图，动点 $M$在以 $O$为圆心， $\mathit{AB}$为直径的半圆弧上运动（点 $M$不与点 $A$、 $B$及 $\stackrel{̂}{\mathit{AB}}$的中点 $F$重合），连接 $\mathit{OM}$．过点 $M$作 $\mathit{ME}\perp \mathit{AB}$于点 $E$，以 $\mathit{BE}$为边在半圆同侧作正方形 $\mathit{BCDE}$，过点 $M$作 $\odot O$的切线交射线 $\mathit{DC}$于点 $N$，连接 $\mathit{BM}$、 $\mathit{BN}$．

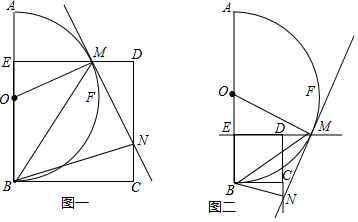
（1）探究：如图一，当动点 $M$在 $\stackrel{̂}{\mathit{AF}}$上运动时；

①判断 $\mathit{\Delta OEM}\backsim \mathit{\Delta MDN}$是否成立？请说明理由；

②设 $\frac{\mathit{ME}+\mathit{NC}}{\mathit{MN}}=k$， $k$是否为定值？若是，求出该定值，若不是，请说明理由；

③设 $\angle \mathit{MBN}=\alpha$， $\alpha$是否为定值？若是，求出该定值，若不是，请说明理由；

（2）拓展：如图二，当动点 $M$在 $\stackrel{̂}{\mathit{FB}}$上运动时；

分别判断（1）中的三个结论是否保持不变？如有变化，请直接写出正确的结论．（均不必说明理由）

已知平面图形 $S$，点 $P$、 $Q$是 $S$上任意两点，我们把线段 $\mathit{PQ}$的长度的最大值称为平面图形 $S$的“宽距”．例如，正方形的宽距等于它的对角线的长度．

（1）写出下列图形的宽距：

①半径为1的圆：　     　；

②如图1，上方是半径为1的半圆，下方是正方形的三条边的“窗户形“：　   　；

（2）如图2，在平面直角坐标系中，已知点 $A(-1,0)$、 $B(1,0)$， $C$是坐标平面内的点，连接 $\mathit{AB}$、 $\mathit{BC}$、 $\mathit{CA}$所形成的图形为 $S$，记 $S$的宽距为 $d$．

①若 $d=2$，用直尺和圆规画出点 $C$所在的区域并求它的面积（所在区域用阴影表示）；

②若点 $C$在 $\odot M$上运动， $\odot M$的半径为1，圆心 $M$在过点 $(0,2)$且与 $y$轴垂直的直线上．对于 $\odot M$上任意点 $C$，都有 $5⩽d⩽8$，直接写出圆心 $M$的横坐标 $x$的取值范围．