初中数学平移的性质解答题

已知反比例函数 $y=\frac{4}{x}$．

（1）若该反比例函数的图象与直线 $y＝\mathit{kx}+4（k\ne 0）$只有一个公共点，求k的值；

（2）如图，反比例函数 $y=\frac{4}{x}（1\le x\le 4）$的图象记为曲线C₁，将C₁向左平移2个单位长度，得曲线C₂，请在图中画出C₂，并直接写出C₁平移至C₂处所扫过的面积．

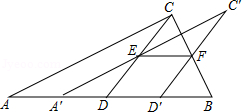
如图，将一张直角三角形ABC纸片沿斜边AB上的中线CD剪开，得到△ACD，再将△ACD沿DB方向平移到△A′C′D′的位置，若平移开始后点D′未到达点B时，A′C′交CD于E，D′C′交CB于点F，连接EF，当四边形EDD′F为菱形时，试探究△A′DE的形状，并判断△A′DE与△EFC′是否全等？请说明理由．

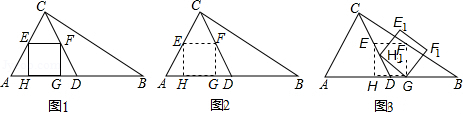
如图1，在△ ABC中，∠ ACB＝90°，∠ B＝30°， AC＝4， D是 AB的中点， EF是△ ACD的中位线，矩形 EFGH的顶点都在△ ACD的边上．

（1）求线段 EF、 FG的长；

（2）如图2，将矩形 EFGH沿 AB向右平移，点 F落在 BC上时停止移动，设矩形移动的距离为 x，矩形与△ CBD重叠部分的面积为 S，求出 S关于 x的函数解析式；

（3）如图3，矩形 EFGH平移停止后，再绕点 G按顺时针方向旋转，当点 H落在 CD边上时停止旋转，此时矩形记作 E ₁ F ₁ GH ₁，设旋转角为α，求cosα的值．

某校开展了一次综合实践活动，参加该活动的每个学生持有两张宽为 $6\mathit{cm}$ ，长足够的矩形纸条．探究两张纸条叠放在一起，重叠部分的形状和面积．

如图1所示，一张纸条水平放置不动，另一张纸条与它成 $45°$ 的角，将该纸条从右往左平移．

（1）写出在平移过程中，重叠部分可能出现的形状．

（2）当重叠部分的形状为如图2所示的四边形 $\mathit{ABCD}$ 时，求证：四边形 $\mathit{ABCD}$ 是菱形．

（3）设平移的距离为 $\mathit{xcm}(0<x⩽6+6\sqrt{2})$ ，两张纸条重叠部分的面积为 $\mathit{sc}{m}^2$ ．求 $s$ 与 $x$ 的函数关系式，并求 $s$ 的最大值．

如图1，抛物线 $y=a{x}^2+\mathit{bx}+3(a\ne 0)$ 与 $x$ 轴的交点 $A(-3,0)$ 和 $B(1,0)$ ，与 $y$ 轴交于点 $C$ ，顶点为 $D$ ．

（1）求该抛物线的解析式；

（2）连接 $\mathit{AD}$ ， $\mathit{DC}$ ， $\mathit{CB}$ ，将 $\mathit{\Delta OBC}$ 沿 $x$ 轴以每秒1个单位长度的速度向左平移，得到△ $O^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}$ ，点 $O$ 、 $B$ 、 $C$ 的对应点分别为点 $O^{\text{'}}$ 、 $B^{\text{'}}$ 、 $C^{\text{'}}$ ，设平移时间为 $t$ 秒，当点 $O^{\text{'}}$ 与点 $A$ 重合时停止移动．记△ $O^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}$ 与四边形 $\mathit{AOCD}$ 重合部分的面积为 $S$ ，请直接写出 $S$ 与 $t$ 之间的函数关系式；

（3）如图2，过该抛物线上任意一点 $M(m,n)$ 向直线 $l:y=\frac{9}{2}$ 作垂线，垂足为 $E$ ，试问在该抛物线的对称轴上是否存在一点 $F$ ，使得 $\mathit{ME}-\mathit{MF}=\frac{1}{4}$ ？若存在，请求出 $F$ 的坐标；若不存在，请说明理由．

如图1，点、点在直线上，反比例函数的图象经过点．

（1）求和的值；

（2）将线段向右平移个单位长度，得到对应线段，连接、．

①如图2，当时，过作轴于点，交反比例函数图象于点，求的值；

②在线段运动过程中，连接，若是以为腰的等腰三角形，求所有满足条件的的值．

在平面直角坐标系中，为原点，点，点在轴的正半轴上，．矩形的顶点，，分别在，，上，．

（Ⅰ）如图①，求点的坐标；

（Ⅱ）将矩形沿轴向右平移，得到矩形，点，，，的对应点分别为，，，．设，矩形与重叠部分的面积为．

①如图②，当矩形与重叠部分为五边形时，，分别与相交于点，，试用含有的式子表示，并直接写出的取值范围；

②当时，求的取值范围（直接写出结果即可）．

如图，直线与双曲线相交于点．已知点，，连接，将沿方向平移，使点移动到点，得到△．过点作轴交双曲线于点．

（1）求与的值；

（2）求直线的表达式；

（3）直接写出线段扫过的面积．

如图1，在平面直角坐标系中，抛物线与直线交于点和点，与轴交于点．

（1）求，的值及抛物线的解析式；

（2）在图1中，把平移，始终保持点的对应点在抛物线上，点，的对应点分别为，，连接，若点恰好在直线上，求线段的长度；

（3）如图2，在抛物线上是否存在点（不与点重合），使和的面积相等？若存在，直接写出点的坐标；若不存在，请说明理由．

一座楼梯的示意图如图所示，要在楼梯上铺一条地毯．

（1）地毯至少需多少长？（用关于a，h的代数式表示）
（2）若楼梯的宽为b，则地毯的面积为多少？
（3）当a=5m，b=1．2m，h=3m时，则地毯的面积是多少m²

（年江西省南昌市）（1）如图1，纸片□ABCD中，AD=5，S_□ABCD=15，过点A作AE⊥BC，垂足为E，沿AE剪下△ABE，将它平移至△DCE′ 的位置，拼成四边形AEE′D，则四边形AEE′D的形状为（    ）
A．平行四边形          B．菱形          C．矩形          D．正方形
（2）如图2，在（1）中的四边形纸片AEE′D中，在EE′上取一点F，使EF=4，剪下△AEF，将它平移至△DE′F′ 的位置，拼成四边形AFF′D．
① 求证四边形AFF′D是菱形；
② 求四边形AFF′D两条对角线的长．