如图,分别是可活动的菱形和平行四边形学具,已知平行四边形较短的边与菱形的边长相等.
(1)在一次数学活动中,某小组学生将菱形的一边与平行四边形较短边重合,摆拼成如图1所示的图形, 经过点 ,连接 交 于点 ,观察发现:点 是 的中点.
下面是两位学生有代表性的证明思路:
思路1:不需作辅助线,直接证三角形全等;
思路2:不证三角形全等,连接 交 于点 .
请参考上面的思路,证明点 是 的中点(只需用一种方法证明);
(2)如图2,在(1)的前提下,当 时,延长 、 交于点 ,求 的值;
(3)在(2)的条件下,若 为大于 的常数),直接用含 的代数式表示 的值.

在现实生活中,我们经常会看到许多“标准”的矩形,如我们的课本封面、 的打印纸等,其实这些矩形的长与宽之比都为 ,我们不妨就把这样的矩形称为“标准矩形”,在“标准矩形” 中, 为 边上一定点,且 ,如图所示.
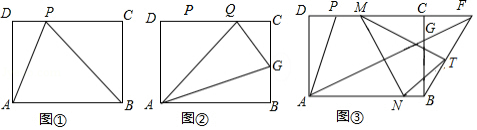
(1)如图①,求证: ;
(2)如图②,点 在 上,且 ,若 为 边上一动点,当 的周长最小时,求 的值;
(3)如图③,已知 ,在(2)的条件下,连接 并延长交 的延长线于点 ,连接 , 为 的中点, 、 分别为线段 与 上的动点,且始终保持 ,请证明: 的面积 为定值,并求出这个定值.
如图,在四边形 中, , , 的平分线 交 于点 , ,点 恰好为 的中点,若 , ,则

A.1B.2C.3D.4
如图,在 中, , ,若进行以下操作,在边 上从左到右依次取点 、 、 、 、 ;过点 作 、 的平行线分别交 、 于点 、 ;过点 作 、 的平行线分别交 、 于点 、 ;过点 作 、 的平行线分别交 、 于点 、 ,则 .

如图,在 中,点 在 边上,连接 ,点 在线段 上, ,且交 于点 , ,且交 于点 ,则下列结论一定正确的是
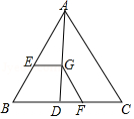
A. B. C. D.
已知正方形 , 为射线 上的一点,以 为边作正方形 ,使点 在线段 的延长线上,连接 , .
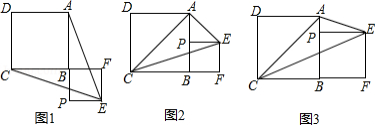
(1)如图1,若点 在线段 的延长线上,求证: ;
(2)如图2,若点 在线段 的中点,连接 ,判断 的形状,并说明理由;
(3)如图3,若点 在线段 上,连接 ,当 平分 时,设 , ,求 及 的度数.
如图,菱形 中,对角线 , 相交于点 , , ,动点 从点 出发,沿线段 以 的速度向点 运动,同时动点 从点 出发,沿线段 以 的速度向点 运动,当其中一个动点停止运动时另一个动点也随之停止.设运动时间为 ,以点 为圆心, 长为半径的 与射线 ,线段 分别交于点 , ,连接 .
(1)求 的长(用含有 的代数式表示),并求出 的取值范围;
(2)当 为何值时,线段 与 相切?
(3)若 与线段 只有一个公共点,求 的取值范围.

试题篮
()