初中数学平行线分线段成比例解答题

如图，一条直线与反比例函数的图象交于A（1，4），B（4，n）两点，与x轴交于点D，AC⊥x轴，垂足为C．
（1）求反比例函数的解析式及D点的坐标；
（2）点P是线段AD的中点，点E，F分别从C，D两点同时出发，以每秒1个单位的速度沿CA，DC运动，到点A，C时停止运动，设运动的时间为t（s）．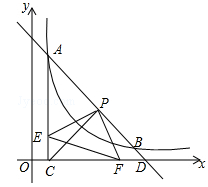

①求证：PE=PF．
②若△PEF的面积为S，求S的最小值．

如图，在平面直角坐标系中，四边形ABCD是菱形，已知A（0，4），B（3，0）．

（1）求D点的坐标；
（2）求经过C点的反比例函数的解析式．

如图，正方形OABC在平面直角坐标系中，点B的坐标是（4，4），O是原点，顶点A、C都在坐标轴上，反比例函数y=（k≠0）在第一象限的图象分别交BC、BA于E、F点（不重合），连接OE、CF相交于点M．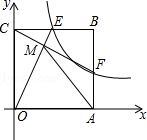

（1）若S_△OEC=4，求直线CF的解析式；
（2）在（1）的情况下，连接AM，求△AMO的面积．

如图，在平面直角坐标系中，已知四边形ABCD为菱形，且A（0，3）、B（﹣4，0）．

（1）求经过点C的反比例函数的解析式；
（2）设P是（1）中所求函数图象上一点，以P、O、A顶点的三角形的面积与△COD的面积相等．求点P的坐标．

直线y=x+b与双曲线y=交于点A（﹣1，﹣5）．并分别与x轴、y轴交于点C、B．

（1）直接写出b=      ，m=      ；
（2）根据图象直接写出不等式x+b＜的解集为      ；
（3）若点D在x轴的正半轴上，是否存在以点D、C、B构成的三角形与△OAB相似？若存在，请求出D的坐标；若不存在，请说明理由．

已知反比例函数y=的图象与一次函数y=kx+m的图象相交于点A（2，1）．

（1）分别求出这两个函数的解析式；
（2）当x取什么范围时，反比例函数值大于0；
（3）若一次函数与反比例函数另一交点为B，且纵坐标为﹣4，当x取什么范围时，反比例函数值大于一次函数的值；
（4）试判断点P（﹣1，5）关于x轴的对称点P′是否在一次函数y=kx+m的图象上．

如图，在平面直角坐标系中，一次函数y=ax+b的图象与反比例函数y=的图象交于一、三象限内的A、B两点，与x轴交于C点，点A的坐标为（2，m），点B的坐标为（n，-2），tan∠BOC=．

（1）求该反比例函数和一次函数的解析式．
（2）求△BOC的面积．
（3）P是x轴上的点，且△PAC的面积与△BOC的面积相等，求P点的坐标．

已知一次函数y=mx+b（m＜0）与反比例函数y=相交于点A（1，3）及点B，当△AOB的面积为4时，求m的值．

已知点A（m，p），B（n，q）（m＜n＜0）在动点C（，a）（k≠0）所形成的曲线上．若p+q=-b-2，．试比较p和q的大小，并说明理由．

如图，将一矩形OABC放在直角坐标系中，O为坐标原点，点A在y轴正半轴上，点E是边AB上的一个动点（不与点A、B重合），过点E的反比例函数y=（x＞0）的图象与边BC交与点F．

（1）若△OAE、△OCF的面积分别为S₁、S₂，且S₁+S₂=2，求k的值；
（2）在（1）的结论下，当OA=2，OC=4时，求三角形OEF的面积．

反比例函数y₁=（x＞0，k≠0）的图象经过点（1，3），P点是直线y₂=-x+6上一个动点，如图所示，设P点的横坐标为m，且满足-m+6＞，过P点分别作PB⊥x轴、PA⊥y轴，垂足分别为B、A，与双曲线分别交于D、C两点，连接OC、OD、CD．

（1）求k的值并结合图象求出m的取值范围；
（2）在P点运动过程中，求线段OC最短时P点的坐标；
（3）将三角形OCD沿着CD翻折，点O的对应点为O′，得到四边形O′COD，问：四边形O′COD能否为菱形？若能，求出P点坐标；若不能，说明理由．

直线y=x+b与双曲线y=交于点A（﹣1，﹣5）．并分别与x轴、y轴交于点C、B．

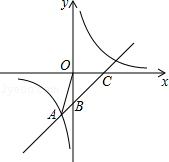
（1）直接写出b=  ，m=  ；
（2）根据图象直接写出不等式x+b＜的解集为         ；
（3）若点D在x轴的正半轴上，是否存在以点D、C、B构成的三角形与△OAB相似？若存在，请求出D的坐标；若不存在，请说明理由．

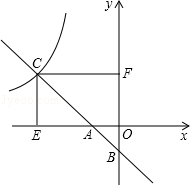
如图，一次函数y₁=mx+n的图象与x轴、y轴分别交于A、B两点，与反比例函数y₂=（x＜0）交于点C，过点C分别作x轴、y轴的垂线，垂足分别为点E、F．若OB=2，CF=6，．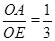

（1）求点A的坐标；
（2）求一次函数和反比例函数的表达式．

如图，点A，D在反比例函数y=（x＞0）的图象上，点A的坐标是（2，4），接AD，过点A作AB⊥AD，交y轴于点B，过点D作DC⊥AD，交x轴于点C，连接BC，四边形ABCD为正方形．

（1）求点C的坐标；
（2）求点D的坐标．

如图，点A在双曲线y=（x＞0）上，过点A作AC⊥x轴，垂足为C，线段OA的垂直平分线BD交x轴于点B，△ABC的周长为4，求点A的坐标．