如图,Rt△ABC中,∠C=90°,BC=6,AC=8.点P,Q都是斜边AB上的动点,点P从B 向A运动(不与点B重合),点Q从A向B运动,BP=AQ.点D,E分别是点A,B以Q,P为对称中心的对称点, HQ⊥AB于Q,交AC于点H.当点E到达顶点A时,P,Q同时停止运动.设BP的长为x,△HDE的面积为y.
(1)求证:△DHQ∽△ABC;
(2)求y关于x的函数解析式并求y的最大值;
如图,在△ABC中,点D、E分别在AB、AC边上,DE∥BC,若AD:DB=1:2,AE=2,则AC= 
如图,等边△ABC的边长为3,点P为BC边上一点,且BP=1,点D为AC上一点;若∠APD=60°,则CD长是 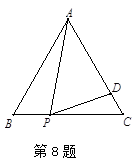
A.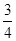 |
B.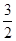 |
C.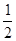 |
D.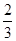 |
含30°角的直角三角板ABC中,∠A=30°.将其绕直角顶点C顺时针旋转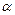 角(
角(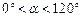 且
且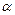 ≠ 90°),得到Rt△
≠ 90°),得到Rt△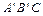 ,
,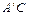 边与AB所在直线交于点D,过点 D作DE∥
边与AB所在直线交于点D,过点 D作DE∥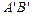 交
交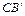 边于点E,连接BE.
边于点E,连接BE.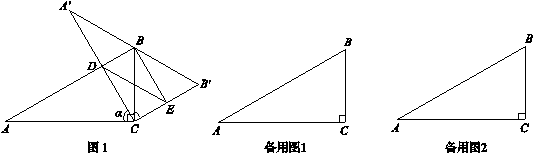
(1)如图1,当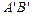 边经过点B时,
边经过点B时,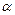 = °;
= °;
(2)在三角板旋转的过程中,若∠CBD的度数是∠CBE度数的m倍,猜想m的值并证明你的结论;
(3) 设 BC=1,AD=x,△BDE的面积为S,以点E为圆心,EB为半径作⊙E,当S=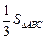
时,求AD的长,并判断此时直线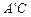 与⊙E的位置关系.
与⊙E的位置关系.
如图,在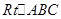 中,∠ACB=90°,BC=3,AC=4,AB的垂直平分线DE交BC的延长线于点E,则CE的长为( )
中,∠ACB=90°,BC=3,AC=4,AB的垂直平分线DE交BC的延长线于点E,则CE的长为( )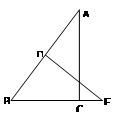
A.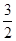 |
B.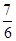 |
C.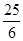 |
D.2 |
如下图,在△ABC中,∠ACB为直角,∠A=30°,CD⊥AB于D。若BD=1,则AB=_____
 和
和 是绕点
是绕点 旋转的两个相似三角形,其中
旋转的两个相似三角形,其中 与
与 、
、 与
与 为对应角.
为对应角.
(1)如图1,若 和
和 分别是以
分别是以 与
与 为顶角的等腰直角三角形,且两三角形旋转到使点
为顶角的等腰直角三角形,且两三角形旋转到使点 、
、 、
、 在同一条直线上的位置时,请直接写出线段
在同一条直线上的位置时,请直接写出线段 与线段
与线段 的关系;
的关系;
(2)若 和
和 为含有
为含有 角的直角三角形,且两个三角形旋转到如图2的位置时,试确定线段
角的直角三角形,且两个三角形旋转到如图2的位置时,试确定线段 与线段
与线段 的关系,并说明理由;
的关系,并说明理由;
(3)若 和
和 为如图3的两个三角形,且
为如图3的两个三角形,且 =
= ,
, ,在绕点
,在绕点 旋转的过程中,直线
旋转的过程中,直线 与
与 夹角的度数是否改变?若不改变,直接用含
夹角的度数是否改变?若不改变,直接用含 、
、 的式子表示夹角的度数;若改变,请说明理由.
的式子表示夹角的度数;若改变,请说明理由.
如果线段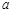 、
、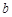 、
、 、
、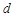 满足
满足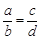 ,那么下列等式不一定成立的是………( ).
,那么下列等式不一定成立的是………( ).
A.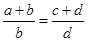 ; ; |
B.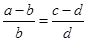 ; ; |
C. ; ; |
D.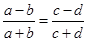 |
已知点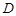 、
、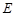 分别在
分别在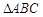 的边
的边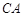 、
、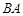 的延长线上,
的延长线上, ∥
∥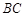 ,
,
若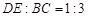 ,则向量
,则向量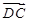 等于……………………………………( ).
等于……………………………………( ).
A.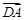 ; ; |
B. ; ; |
C.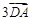 ; ; |
D.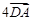 . . |
如图D、E分别在△ABC的边AB、AC上,要使△AED∽△ABC,应添加条件是 ;(只写出一种即可)
试题篮
()