王华同学在晚上由路灯AC走向路灯BD,当他走到点P时,发现身后他影子的顶部刚好接触到路灯AC的底部,当他向前再步行12m到达Q点时,发现身前他影子的顶部刚好接触到路灯BD的底部.已知王华同学的身高是1.6m,两个路灯的高度都是9.6m.
求两个路灯之间的距离;(考查投影及相似三角形中的比例计算)
当王华同学走到路灯BD处时,他在路灯AC下的影子长是多少?
如图,△ABC中,AB=AC,过点A作GE∥BC,角平分线BD、CF相交于点H,它们的延长线分别交GE于点E、G.试在图中找出3对全等三角形,并对其中一对全等三角形给出证明.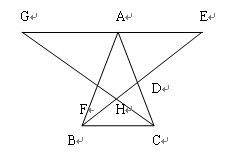
已知:AB是⊙O的直径,弦CD⊥AB于点G,E是直线AB上一动点(不与点A、B、G重合),直线DE交⊙O于点F,直线CF交直线AB于点P.设⊙O的半径为r.
(1)如图1,当点E在直径AB上时,试证明:OE·OP=r2
(2)当点E在AB(或BA)的延长线上时,以如图2点E的位置为例,请你画出符合题意的图形,标注上字母,(1)中的结论是否成立?请说明理由.
(本题8分)如图,在Rt△ABC中,AC=4,BC=3.在Rt△ABC内并排放入(不重叠)n个小正方形纸片,使这些纸片的一边都在AB上,首尾两个正方形各有一个顶点D、E分别在AC、BC上,求小正方形的边长(用n的代数式表示)。
(1)请在方格纸上建立平面直角坐标系,使
 ,并求出
,并求出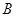 点坐标;
点坐标;(2)以原点
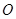 为位似中心,相似比为2:1,在第一象限内将
为位似中心,相似比为2:1,在第一象限内将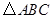 放大,画出放大后的图形
放大,画出放大后的图形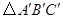 ;
;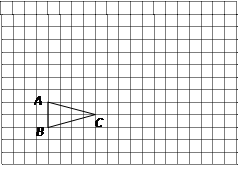
如图,已知每个小方格都是边长为1的正方形,我们称每个小正方形的顶点为格点,以格点为顶点的图形称为格点图形. 图中的△ABC是一个格点三角形.
请你在第一象限内画出格点△AB1C1,使得△AB1C1∽△ABC,且△AB1C1与△ABC的相似比为3:1;
写出B1、C1两点的坐标.
已知:把Rt△ABC和Rt△DEF按如图甲摆放(点C与点E重合),点B、C(E)、F在同一条直线上.∠BAC = ∠DEF = 90°,∠ABC = 45°,BC =" 9" cm,DE =" 6" cm,EF =" 8" cm.
如图乙,△DEF从图甲的位置出发,以1 cm/s的速度沿CB向△ABC匀速移动,在△DEF移动的同时,点P从△DEF的顶点F出发,以3 cm/s的速度沿FD向点D匀速移动.当点P移动到点D时,P点停止移动,△DEF也随之停止移动.DE与AC相交于点Q,连接BQ、PQ,设移动时间为t(s).解答下列问题:设三角形BQE的面积为y(cm2),求y与t之间的函数关系式,并写出自变量t的取值范围;
当t为何值时,三角形DPQ为等腰三角形?
是否存在某一时刻t,使P、Q、B三点在同一条直线上?若存在,求出此时t的值;若不存在,说明理由


如图,上体育课,甲、乙两名同学分别站在C、D的位置时,乙的影子恰好在甲的影子里边,已知甲,乙同学相距1米.甲身高1.8米,乙身高 1.5米,则甲的影长是多少米?
1.5米,则甲的影长是多少米?
半径为5的⊙O中,直径AB的不同侧有定点C和动点P. 已知BC∶CA=4∶3,点P在弧AB上运动,过点C作CP的垂线,与PB的延长线交于点Q. 求证:△ABC∽△PQC;
当点P与点C关于AB对称时,求CQ的长;
当点P运动到什么位置时,CQ取到最大值?求此时CQ的长;
当点P运动到弧AB的中点时,求CQ的长.
已知正方形纸片 的边长为2.操作:如图1,将正方形纸片折叠,使顶点
的边长为2.操作:如图1,将正方形纸片折叠,使顶点 落在边
落在边 上的点
上的点 处(点
处(点 与
与 、
、 不重合),折痕为
不重合),折痕为 ,折叠后
,折叠后 边落在
边落在 的位置,
的位置, 与
与 交于点
交于点 .
.
探究:观察操作结果,找到一个与
 相似的三角形,并证明你的结论;
相似的三角形,并证明你的结论;当点
 位于
位于 中点时,你找到的三角形与
中点时,你找到的三角形与 周长的比是多少(图2为备用图)?
周长的比是多少(图2为备用图)?
如图,在矩形ABCD中,AB=3cm,AD=4cm,点E是BC上一动点(不与B、C重合),且DF⊥AE,垂足为F. 设AE=xcm,DF=ycm.(1)求证:△DFA∽△ABE;
(2)试求y与x之间的函数关系式,并求出自变量的取值范围.


试题篮
()