△ABC是一块锐角三角形余料，边BC＝180 mm，高AD＝120 mm，要把它加工成矩形零件，使一边在BC上，其余两个顶点分别在边AB、AC上．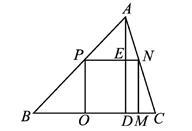
（1）若这个矩形是正方形，那么边长是多少？
（2）若这个矩形的长是宽的2倍，则边长是多少？
已知：如图，在平面直角坐标系中，O为坐标原点，△OAB的顶点A、B的坐标分别是A（0，5），B（3，1），过点B画BC⊥AB交直线y=﹣m（m＞
）于点C，连结AC，以点A为圆心，AC为半径画弧交x轴负半轴于点D，连结AD、CD．
（1）求证：△ABC≌△AOD；
（2）设△ACD的面积为S，求S关于m的函数关系式；
（3）若四边形ABCD恰有一组对边平行，求m的值．
【提出问题】如图1，小东将一张AD为12，宽AB为4的长方形纸片按如下方式进行折叠：在纸片的一边BC上分别取点P、Q，使得BP=CQ，连结AP、DQ，将△ABP、△DCQ分别沿AP、DQ折叠得△APM，△DQN，连结MN．小东发现线段MN的位置和长度随着点P、Q的位置发生改变．
【规律探索】
（1）请在图1中过点M，N分别画ME⊥BC于点E，NF⊥BC于点F．
求证：①ME=NF；②MN∥BC．
【解决问题】
（2）如图1，若BP=3，求线段MN的长；
（3）如图2，当点P与点Q重合时，求MN的长．
在Rt△ABC中，∠ACB=90°，tan∠BAC=
．点D在边AC上（不与A，C重合），连接BD，F为BD中点．
（1）若过点D作DE⊥AB于E，连接CF、EF、CE，如图1．设CF=kEF，则k= ；
（2）若将图1中的△ADE绕点A旋转，使得D、E、B三点共线，点F仍为BD中点，如图2所示．求证：BE-DE=2CF；
（3）若BC=6，点D在边AC的三等分点处，将线段AD绕点A旋转，点F始终为BD中点，求线段CF长度的最大值．
如图的⊙O中，AB为直径，OC⊥AB，弦CD与OB交于点F，过点D、A分别作⊙O的切线交于点G，并与AB延长线交于点E．
（1）求证：∠1=∠2．
（2）已知：OF：OB=1：3，⊙O的半径为3，求AG的长．
如图，在矩形ABCD中，AB=2AD，线段EF=10．在EF上取一点M，分别以EM、MF为一边作矩形EMNH、矩形MFGN，使矩形MFGN∽矩形ABCD．令MN=x，当x为何值时，矩形EMNH的面积S有最大值，最大值是多少？
如图，光源L距地面（LN）8米，距正方体大箱顶站（LM）2米，已知，在光源照射下，箱子在左侧的影子BE长5米，求箱子在右侧的影子CF的长．（箱子边长为6米）
在梯形ABCD中，AD∥BC，∠D=90°，以AB为直径作⊙O．
（1）如图①，⊙O与DC相切于点E，
①求证：∠BAE=∠DAE；②若AB=6，求AD+BC的值．
（2）如图②，⊙O与DC交于点E、F．
①图中哪一个角与∠BAE相等？为什么？②试探究线段DF与CE的数量关系，并说明理由．
如图1，将一个直角三角板的直角顶点P放在正方形ABCD的对角线BD上滑动，并使其一条直角边始终经过点A，另一条直角边与BC相交于点E．
（1）求证：PA=PE；
（2）若将（1）中的正方形变为矩形，其余条件不变（如图2），且AD=10，DC=8，求AP：PE；
（3）在（2）的条件下，当P滑动到BD的延长线上时（如图3），请你直接写出AP：PE的比值．
在Rt△ABC中，∠ACB=90°，AC=2，BC=4．点D是线段BC上的一个动点．点D与点B、C不重合，过点D作DE⊥BC交AB于点E，将△ABC沿着直线DE翻折，使点B落在直线BC上的F点．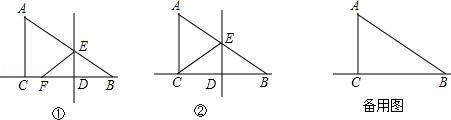
（1）设∠BAC=α（如图①），求∠AEF的大小；（用含α的代数式表示）
（2）当点F与点C重合时（如图②），求线段DE的长度；
（3）设BD=x，△EDF与△ABC重叠部分的面积为S，试求出S与x之间函数关系式，并写出自变量x的取值范围．
如图，已知：矩形ABCD，以对角线AC的中点O为圆心，OA的长为半径作⊙O，⊙O经过B、D两点，过点B作BK⊥AC，垂足为点K，过点D作DH∥KB，DH分别与AC、AB、⊙O及CB的延长线相交于点E、F、G、H．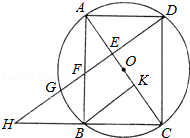
（1）求证：AE=CK；
（2）若F是EG的中点，且DE=6，求⊙O的半径．
如图，在Rt△ACB中，∠C=90°，AC=8cm，BC=6cm，点P、Q同时由A、B两点出发分别沿AC、BC向点C匀速移动，它们的速度都是1米/秒，问：几秒后△PCQ的面积为Rt△ACB面积的一半？
试题篮
()
粤公网安备 44130202000953号
