如图,矩形OABC在平面直角坐标系中,O为坐标原点,点A(0,4),C(2,0),将矩形OABC绕点O按顺时针方向旋转1800,得到矩形OEFG,顺次连接AC、CE、EG、GA.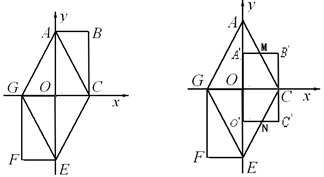
(1)请直接写出点F的坐标;
(2)试判断四边形ACEG的形状,并说明理由;
(3)将矩形OABC沿y轴向下平移m个单位(0<m<4),设平移过程中矩形与 重叠部分面积为
重叠部分面积为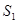 ,当
,当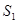 :
: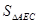 =11:16时,求m的值.
=11:16时,求m的值.
如图,PB为⊙O的切线,B为切点,直线PO交⊙于点E,F,过点B作PO的垂线BA,垂足为点D,交⊙O于点A,延长AO与⊙O交于点C,连接BC,AF.
(1)求证:直线PA为⊙O的切线;
(2)试探究线段EF,OD,OP之间的等量关系,并加以证明;
(3)若BC=6,tan∠F= ,求cos∠ACB的值和线段PE的长.
,求cos∠ACB的值和线段PE的长.
已知△ABC是等腰直角三角形,∠A=90°,点D是腰AC上的一个动点,过C作CE垂直于BD的延长线,垂足为E.
(1)若BD是AC边上的中线,如图1,求 的值;
的值;
(2)若BD是∠ABC的角平分线,如图2,求 的值.
的值.
如图,在△ABC中,∠C=90°,CD⊥AB,垂足为D,AC=20,BC=15.动点P从A开始,以每秒2个单位长的速度沿AB方向向终点B运动,过点P分别作AC、BC边的垂线,垂足为E、F.
(1)求AB与CD的长;
(2)当矩形PECF的面积最大时,求点P运动的时间t;
(3)以点C为圆心,r为半径画圆,若圆C与斜边AB有且只有一个公共点时,求r的取值范围.
如图,直线AB分别与两坐标轴交于点A(4,0).B(0,8),点C的坐标为(2,0).
(1)求直线AB的解析式;
(2)在线段AB上有一动点P.
①过点P分别作x,y轴的垂线,垂足分别为点E,F,若矩形OEPF的面积为6,求点P的坐标.
②连结CP,是否存在点P,使 与
与 相似,若存在,求出点P的坐标,若不存在,请说明理由.
相似,若存在,求出点P的坐标,若不存在,请说明理由.
已知:如图①,在Rt△ACB中,∠C=90º,AC=6cm,BC=8cm,点P由B出发沿BC方向向点C匀速运动,速度为2cm/s;点Q由A出发沿AB方向向点B匀速运动,速度为1cm/s;连接PQ.若设运动的时间为t(s)(0<t<4),解答下列问题:

(1)当t为何值时,PQ的垂直平分线经过点B?
(2)如图②,连接CQ.设△PQC的面积为y(cm2),求y与t之间的函数关系式;

(3)如图②,是否存在某一时刻t,使线段C Q恰好把四边形ACPQ的面积分成1:2的两部分?若存在,求出此时t的值;若不存在,说明理由.
提出问题:如图①,在四边形ABCD中,点E、F是AD的n等分点中最中间2个,点G、H是BC的n等分点中最中间2个,(其中n为奇数),连接EG、FH,那么S四边形EFHG与S四边形ABCD之间有什么关系呢?
探究发现:为了解决这个问题,我们可以先从一些简单的、特殊的情形入手:
(1)如图②:四边形ABCD中,点E、F是AD的3等分点,点G、H是BC的3等分点,连接EG、FH,那么S四边形EFHG与S四边形ABCD之间有什么关系呢?
如图③,连接EH、BE、DH,
因为△EGH与△EBH高相等,底的比是1:2,
所以S△EGH= S△EBH
S△EBH
因为△EFH与△DEH高相等,底的比是1:2,
所以S△EFH= S△DEH
S△DEH
所以S△EGH+S△EFH= S△EBH +
S△EBH + S△DEH
S△DEH
即S四边形EFHG= S四边形EBHD
S四边形EBHD
连接BD,
因为△DBE与△ABD高相等,底的比是2:3,
所以S△DBE= S△ABD
S△ABD
因为△BDH与△BCD高相等,底的比是2:3,
所以S△BDH= S△BCD
S△BCD
所以S△DBE +S△BDH= S△ABD+
S△ABD+ S△BCD =
S△BCD = (S△ABD+S△BCD)
(S△ABD+S△BCD)
= S四边形ABCD
S四边形ABCD
即S四边形EBHD= S四边形ABCD
S四边形ABCD
所以S四边形EFHG= S四边形EBHD=
S四边形EBHD= ×
× S四边形ABCD=
S四边形ABCD= S四边形ABCD
S四边形ABCD
(1)如图④:四边形ABCD中,点E、F是AD的5等分点中最中间2个,点G、H是BC的5等分点中最中间2个,连接EG、FH,猜想:S四边形EFHG与S四边形ABCD之间有什么关系呢
验证你的猜想:
(2)问题解决:如图①,在四边形ABCD中,点E、F是AD的n等分点中最中间2个,点G、H是BC的n等分点中最中间2个,连接EG、FH,(其中n为奇数)
那么S四边形EFHG与S四边形ABCD之间的关系为: (不必写出求解过程)
如图,在△ABC中,AB=AC,以AB为直径作半圆⊙0,交BC于点D,连接AD,过点D作DE⊥AC,垂足为点E,交AB的延长线于点F.
(1)求证:EF是⊙0的切线.(2)如果⊙0的半径为5,sin∠ADE= ,求BF的长.
,求BF的长.
如图,在直角梯形OABC中,OA∥BC,A、B两点的坐标分别为A(13,0),B(11,12),动点P,Q分别从O、B两点同时出发,点P以每秒2个单位的速度沿OA向终点A运动,点Q以每秒1个单位的速度沿BC向C运动,当点P停止运动时,点Q同时停止运动.线段OB、PQ相交于点D,过点D作DE∥OA,交AB于点E,设动点P、Q运动时间为t(单位:s)
(1)当t为何值时,四边形PABQ是平行四边形,请写出推理过程;
(2)通过推理论证:在P、Q的运动过程中,线段DE的长度不变;
如图,抛物线y=ax2+bx+c与x轴的一个交点A的坐标为(﹣1,0),对称轴为直线x=﹣2.
(1)求抛物线与x轴的另一个交点B的坐标;
(2)点D是抛物线与y轴的交点,点C是抛物线上的另一点.若以AB为一底边的梯形ABCD的面积为9.
求此抛物线的解析式,并指出顶点E的坐标;
(3)点P是(2)中抛物线对称轴上一动点,且以1个单位/秒的速度从此抛物线的顶点E向上运动.设点P运动的时间为t秒.
①当t为 秒时,△PAD的周长最小?当t为 秒时,△PAD是以AD为腰的等腰三角形?(结果保留根号)
②点P在运动过程中,是否存在一点P,使△PAD是以AD为斜边的直角三角形?若存在,求出点P的坐标;若不存在,请说明理由.
小明对直角三角形很感兴趣. △ABC中,∠ACB=90°,D是AB上任意一点,连接DC,作DE⊥DC,EA⊥AC,DE与AE交于点E.请你跟着他一起解决下列问题:
(1)如图1,若△ABC是等腰直角三角形,则DE,DC有什么数量关系?请给出证明.
(2)如果换一个直角三角形,如图2,∠CBA=30°,则DE,DC又有什么数量关系?请给出证明.
(3)由(1)、(2)这两种特殊情况,小明提出问题:如果直角三角形ABC中,BC=mAC,那DE, DC有什么数量关系?请给出证明.
如图,在△ABC中,∠B= 90°,点P从A点开始沿AB边向点B以1厘米/秒的速度移动,点Q从B点开始沿BC边向点C以2厘米/秒的速度移动。
(1)如果P、Q分别从A、B两点同时出发,经过几秒钟,△PBQ的面积等于8厘米2?
(2)如果P、Q两分别从A、B两点同时出发,并且P到B又继续在BC边上前进,Q到C后又继续在CA边上前进,经过几秒钟,△PCQ的面积等于12﹒6厘米2 ?
如图,在平面直角坐标系中,点 的坐标为
的坐标为 ,点
,点 在
在 轴上,
轴上, 是线段
是线段 的中点.将线段
的中点.将线段 绕着点
绕着点 顺时针方向旋转
顺时针方向旋转 ,得到线段
,得到线段 ,连结
,连结 、
、 .
.
(1)判断 的形状,并简要说明理由;
的形状,并简要说明理由;
(2)当 时,试问:以
时,试问:以 、
、 、
、 、
、 为顶点的四边形能否为平行四边形?若能,求出相应的
为顶点的四边形能否为平行四边形?若能,求出相应的 的值?若不能,请说明理由;
的值?若不能,请说明理由;
(3)当 为何值时,
为何值时, 与
与 相似?
相似?
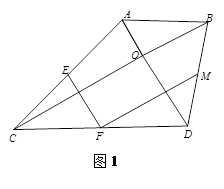
以平面上一点O为直角顶点,分别画出两个直角三角形,记作△AOB和△COD,其中∠ABO=∠DCO=30°.
(1)点E、F、M分别是AC、CD、DB的中点,连接EF和FM.
①如图1,当点D、C分别在AO、BO的延长线上时,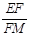 =_______;
=_______;
②如图2,将图1中的△AOB绕点O沿顺时针方向旋转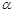 角(
角( ),其他条件不变,判断
),其他条件不变,判断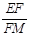 的值是否发生变化,并对你的结论进行证明;
的值是否发生变化,并对你的结论进行证明;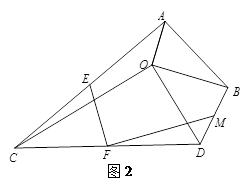
(2)如图3,若BO= ,点N在线段OD上,且NO=3.点P是线段AB上的一个动点,在将△AOB绕点O旋转的过程中,线段PN长度的最小值为_______,最大值为_______.
,点N在线段OD上,且NO=3.点P是线段AB上的一个动点,在将△AOB绕点O旋转的过程中,线段PN长度的最小值为_______,最大值为_______.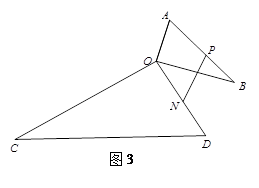
如图,AB是⊙O的直径,C是⊙O上一点,AD垂直于过点C的直线,垂足为D,且AC平分∠BAD.
(1)求证:CD是⊙O的切线;
(2)若AC= ,AD=4,求AB的长.
,AD=4,求AB的长.
试题篮
()