如图,在直角坐标系中,矩形 的顶点
的顶点 与坐标原点重合,顶点
与坐标原点重合,顶点 在坐标轴上,
在坐标轴上, ,
, .动点
.动点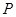 从点
从点 出发,以
出发,以 的速度沿
的速度沿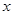 轴匀速向点
轴匀速向点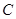 运动,到达点
运动,到达点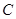 即停止.设点
即停止.设点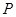 运动的时间为
运动的时间为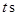 .
.
(1)过点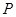 作对角线
作对角线 的垂线,垂足为点
的垂线,垂足为点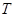 .求
.求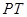 的长
的长 与时间
与时间 的函数关系式,并写出自变量
的函数关系式,并写出自变量 的取值范围;
的取值范围;
(2)在点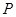 运动过程中,当点
运动过程中,当点 关于直线
关于直线 的对称点
的对称点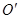 恰好落在对角线
恰好落在对角线 上时,求此时直线
上时,求此时直线 的函数解析式;
的函数解析式;
(3)探索:以 三点为顶点的
三点为顶点的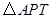 的面积能否达到矩形
的面积能否达到矩形 面积的
面积的 ?请说明理由.
?请说明理由.
如图1,点 将线段
将线段 分成两部分,如果
分成两部分,如果 ,那么称点
,那么称点 为线段
为线段 的黄金分割点.
的黄金分割点.
某研究小组在进行课题学习时,由黄金分割点联想到“黄金分割线”,类似地给出“黄金分割线”的定义:直线 将一个面积为
将一个面积为 的图形分成两部分,这两部分的面积分别为
的图形分成两部分,这两部分的面积分别为 ,
, ,如果
,如果 ,那么称直线
,那么称直线 为该图形的黄金分割线.
为该图形的黄金分割线.
(1)研究小组猜想:在 中,若点
中,若点 为
为 边上的黄金分割点(如图2),则直线
边上的黄金分割点(如图2),则直线 是
是 的黄金分割线.你认为对吗?为什么?
的黄金分割线.你认为对吗?为什么?
(2)请你说明:三角形的中线是否也是该三角形的黄金分割线?
(3)研究小组在进一步探究中发现:过点 任作一条直线交
任作一条直线交 于点
于点 ,再过点
,再过点 作直线
作直线 ,交
,交 于点
于点 ,连接
,连接 (如图3),则直线
(如图3),则直线 也是
也是 的黄金分割线.
的黄金分割线.
请你说明理由.
(4)如图4,点 是
是 的边
的边 的黄金分割点,过点
的黄金分割点,过点 作
作 ,交
,交 于点
于点 ,显然直线
,显然直线 是
是 的黄金分割线.请你画一条
的黄金分割线.请你画一条 的黄金分割线,使它不经过
的黄金分割线,使它不经过 各边黄金分割点.
各边黄金分割点.
在平面内,先将一个多边形以点 为位似中心放大或缩小,使所得多边形与原多边形对应线段的比为
为位似中心放大或缩小,使所得多边形与原多边形对应线段的比为 ,并且原多边形上的任一点
,并且原多边形上的任一点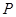 ,它的对应点
,它的对应点 在线段
在线段 或其延长线上;接着将所得多边形以点
或其延长线上;接着将所得多边形以点 为旋转中心,逆时针旋转一个角度
为旋转中心,逆时针旋转一个角度 ,这种经过和旋转的图形变换叫做旋转相似变换,记为
,这种经过和旋转的图形变换叫做旋转相似变换,记为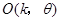 ,其中点
,其中点 叫做旋转相似中心,
叫做旋转相似中心, 叫做相似比,
叫做相似比, 叫做旋转角.
叫做旋转角.
(1)填空:
①如图1,将 以点
以点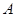 为旋转相似中心,放大为原来的2倍,再逆时针旋转
为旋转相似中心,放大为原来的2倍,再逆时针旋转 ,得到
,得到 ,这个旋转相似变换记为
,这个旋转相似变换记为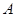 ( , );
( , );
②如图2, 是边长为
是边长为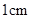 的等边三角形,将它作旋转相似变换
的等边三角形,将它作旋转相似变换 ,得到
,得到 ,则线段
,则线段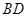 的长为
的长为  ;
;
(2)如图3,分别以锐角三角形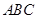 的三边
的三边 ,
,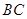 ,
, 为边向外作正方形
为边向外作正方形 ,
, ,
,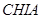 ,点
,点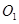 ,
, ,
, 分别是这三个正方形的对角线交点,试分别利用
分别是这三个正方形的对角线交点,试分别利用 与
与 ,
, 与
与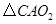 之间的关系,运用旋转相似变换的知识说明线段
之间的关系,运用旋转相似变换的知识说明线段 与
与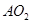 之间的关系.
之间的关系.
如图,在平面直角坐标系中,点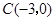 ,点
,点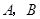 分别在
分别在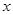 轴,
轴,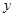 轴的正半轴上,且满足
轴的正半轴上,且满足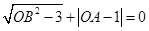 .
.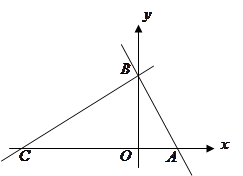
(1)求点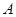 ,点
,点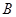 的坐标.
的坐标.
(2)若点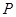 从
从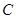 点出发,以每秒1个单位的速度沿射线
点出发,以每秒1个单位的速度沿射线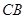 运动,连结
运动,连结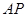 .设
.设 的面积为
的面积为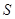 ,点
,点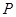 的运动时间为
的运动时间为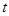 秒,求
秒,求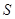 与
与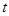 的函数关系式,并写出自变量的取值范围.
的函数关系式,并写出自变量的取值范围.
(3)在(2)的条件下,是否存在点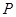 ,使以点
,使以点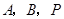 为顶点的三角形与
为顶点的三角形与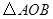 相似?若存在,请直接写出点
相似?若存在,请直接写出点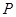 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
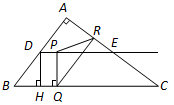
如图,在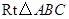 中,
中,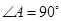 ,
,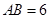 ,
,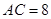 ,
,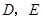 分别是边
分别是边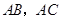 的中点,点
的中点,点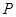 从点
从点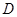 出发沿
出发沿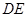 方向运动,过点
方向运动,过点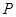 作
作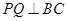 于
于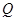 ,过点
,过点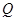 作
作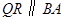 交
交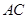 于
于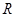 ,当点
,当点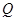 与点
与点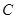 重合时,点
重合时,点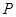 停止运动.设
停止运动.设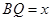 ,
,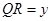 .
.
(1)求点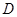 到
到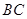 的距离
的距离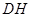 的长;
的长;
(2)求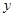 关于
关于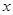 的函数关系式(不要求写出自变量的取值范围);
的函数关系式(不要求写出自变量的取值范围);
(3)是否存在点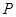 ,使
,使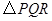 为等腰三角形?若存在,请求出所有满足要求的
为等腰三角形?若存在,请求出所有满足要求的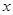 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
如图,在平面直角坐标系中,直角梯形OABC的边OC、OA分别与x轴、y轴重合,AB∥OC,∠AOC=90°,∠BCO=45°,BC=12 ,点C的坐标为(-18,0)。
,点C的坐标为(-18,0)。
(1)求点B的坐标;
(2)若直线DE交梯形对角线BO于点D,交y轴于点E,且OE=4,OD=2BD,求直线DE的解析式;
(3)若点P是(2)中直线DE上的一个动点,在坐标平面内是否存在点Q,使以O、E、P、Q为顶点的四边形是菱形?若存在,请直接写出点Q的坐标;若不存在,请说明理由。
如图,在平面直角坐标系中,已知Rt△AOB的两条直角边0A、08分别在y轴和x轴上,并且OA、OB的长分别是方程x2—7x+12=0的两根(OA<0B),动点P从点A开始在线段AO上以每秒l个单位长度的速度向点O运动;同时,动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A运动,设点P、Q运动的时间为t秒.
(1)求A、B两点的坐标。
(2)求当t为何值时,△APQ与△AOB相似,并直接写出此时点Q的坐标.
(3)当t=2时,在坐标平面内,是否存在点M,使以A、P、Q、M为顶点的四边形是平行四边形?若存在,请直接写出M点的坐标;若不存在,请说明理由.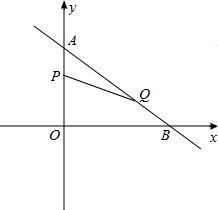
已知:正方形 的边长为1,射线
的边长为1,射线 与射线
与射线 交于点
交于点 ,射线
,射线 与射线
与射线 交于点
交于点 ,
, .
.
(1)如图1,当点 在线段
在线段 上时,试猜想线段
上时,试猜想线段 、
、 、
、 有怎样的数量关系?并证明你的猜想.
有怎样的数量关系?并证明你的猜想.
(2)设 ,
, ,当点
,当点 在线段
在线段 上运动时(不包括点
上运动时(不包括点 、
、 ),如图1,求
),如图1,求 关于
关于 的函数解析式,并指出
的函数解析式,并指出 的取值范围.
的取值范围.
(3)当点 在射线
在射线 上运动时(不含端点
上运动时(不含端点 ),点
),点 在射线
在射线 上运动.试判断以
上运动.试判断以 为圆心以
为圆心以 为半径的
为半径的 和以
和以 为圆心以
为圆心以 为半径的
为半径的 之间的位置关系.
之间的位置关系.
(4)当点 在
在 延长线上时,设
延长线上时,设 与
与 交于点
交于点 ,如图2.问△
,如图2.问△ 与△
与△ 能否相似,若能相似,求出
能否相似,若能相似,求出 的值,若不可能相似,请说明理由.
的值,若不可能相似,请说明理由.
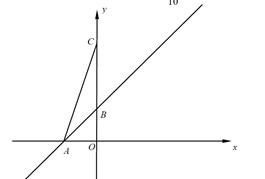
如图,直线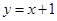 与
与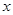 轴、
轴、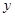 轴分别相交于点
轴分别相交于点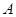 、
、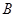 .抛物线
.抛物线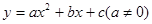 与
与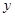 轴的正半轴相交于点
轴的正半轴相交于点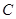 ,与这个一次函数的图像相交于
,与这个一次函数的图像相交于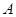 、
、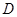 ,且
,且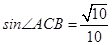 .
.
(1)求点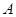 、
、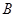 、
、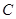 的坐标;
的坐标;
(2)如果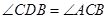 ,求抛物线
,求抛物线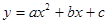 的解析式.
的解析式.
如图,在△ABC中,∠C=90º,AC=6cm,BC=8cm,D、E分别是AC、AB
的中点,连接DE.点P从点D出发,沿DE方向匀速运动,速度为1cm/s;同时,点Q从点B出发,沿
BA方向匀速运动,速度为2cm/s,当点P停止运动时,点Q也停止运动.连接PQ,设运动时间为t(0<t
<4)s.解答下列问题:

(1)当t为何值时,PQ⊥AB?
(2)当点Q在B、E之间运动时,设五边形PQBCD的面积为ycm2,求y与t之间的函数关系式;
(3)在(2)的情况下,是否存在某一时刻t,使得PQ分四边形BCDE所成的两部分的面积之比为
 =1∶29?若存在,求出此时t的值以及点E到PQ的距离h;若不存在,请说明理由.
=1∶29?若存在,求出此时t的值以及点E到PQ的距离h;若不存在,请说明理由.
如图1,已知△ABC中,AB=10cm,AC=8cm,BC=6cm.如果点P由B出发沿BA方向点A匀速运动,同时点Q由A出发沿AC方向向点C匀速运动,它们的速度均为2cm/s.连接PQ,设运动的时间为t(单位:s)(0≤t≤4).解答下列问题:
(1)当t为何值时,PQ∥BC.
(2)设△AQP面积为S(单位:cm2),当t为何值时,S取得最大值,并求出最大值.
(3)是否存在某时刻t,使线段PQ恰好把△ABC的面积平分?若存在,求出此时t的值;若不存在,请说明理由.
(4)如图2,把△AQP沿AP翻折,得到四边形AQPQ′.那么是否存在某时刻t,使四边形AQPQ′为菱形?若存在,求出此时菱形的面积;若不存在,请说明理由.
定义:P、Q分别是两条线段a和b上任意一点,线段PQ长度的最小值叫做线段与线段的距离.
已知O(0,0),A(4,0),B(m,n),C(m+4,n)是平面直角系中四点.
(1)根据上述定义,当m=2,n=2时,如图1,线段BC与线段OA的距离是_____,
当m=5,n=2时,如图2,线段BC与线段OA的距离(即线段AB的长)为______


(2)如图3,若点B落在圆心为A,半径为2的圆上,线段BC与线段OA的距离记为d,求d关于m的函数解析式.
(3)当m的值变化时,动线段BC与线段OA的距离始终为2,线段BC的中点为M.
①求出点M随线段BC运动所围成的封闭图形的周长;
②点D的坐标为(0,2),m≥0,n≥0,作MH⊥x轴,垂足为H,是否存在m的值,使以A、M、H为顶点的三角形与△AOD相似,若存在,求出m的值;若不存在,请说明理由.

如图,在△ABC中,AB=AC,∠B=30°,BC=8,D在边BC上,E在线段DC上,DE=4,△DEF是等边三角形,边DF交边AB于点M,边EF交边AC于点N.
(1)求证:△BMD∽△CNE;
(2)当BD为何值时,以M为圆心,以MF为半径的圆与BC相切?
(3)设BD=x,五边形ANEDM的面积为y,求y与x之间的函数解析式(要求写出自变量x的取值范围);当x为何值时,y有最大值?并求y的最大值.
小明想利用太阳光测量楼高,他带着皮尺来到一栋楼下,发现对面墙上有这栋楼的影子,针对这种情况,他设计了一种测量方案,具体测量情况如下:
如示意图,小明边移动边观察,发现站到点E处时,可以使自己落在墙上的影子与这栋楼落在墙上的影子重叠,且高度恰好相同.此时,测得小明落在墙上的影子高度CD=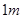 ,CE=
,CE= ,CA=
,CA=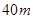 (点A、E、C在同一直线上).已知小明的身高EF是
(点A、E、C在同一直线上).已知小明的身高EF是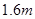 ,请你帮小明求出楼高AB.
,请你帮小明求出楼高AB.
如图,边长为4的等边△AOB的顶点O在坐标原点,点A在x轴正半轴上,点B在第一象限.一动点P沿x轴以每秒1个单位长度的速度由点O向点A匀速运动,当点P到达点A时停止运动,设点P运动的时间是t秒.在点P的运动过程中,线段BP的中点为点E,将线段PE绕点P按顺时针方向旋转60º得PC.
(1)当点P运动到线段OA的中点时, 点C的坐标为 ;
(2)在点P从点O到点A的运动过程中,用含t的代数式表示点C的坐标;
(3)在点P从点O到点A的运动过程中,求出点C所经过的路径长.

试题篮
()