初中数学相似多边形的性质解答题

如图，在四边形ABCD中，∠BAC=∠ACD=90°，∠B=∠D．
（1）求证：四边形ABCD是平行四边形；
（2）若AB=3cm，BC=5cm，AE=AB，点P从B点出发，以1cm/s的速度沿BC→CD→DA运动至A点停止，则从运动开始经过多少时间，△BEP为等腰三角形？

如图，AD是ABC的高，点P，Q在BC边上，点R在AC边上，点S在AB边上，BC=60cm，AD=40cm，AB=AC.四边形PQRS是正方形。
（1）ASR与ABC相似吗？为什么？
（2）求正方形PQRS的边长。

情境观察将矩形ABCD纸片沿对角线AC剪开，得到△ABC和△A′C′D，如图1所示．将△A′C′D的顶点A′与点A重合，并绕点A按逆时针方向旋转，使点D、A（A′）、B在同一条直线上，如图2所示．
观察图2可知：与BC相等的线段是　_________　，∠CAC′=　_________　°．

问题探究
如图3，△ABC中，AG⊥BC于点G，以A为直角顶点，分别以AB、AC为直角边，向△ABC外作等腰Rt△ABE和等腰Rt△ACF，过点E、F作射线GA的垂线，垂足分别为P、Q．试探究EP与FQ之间的数量关系，并证明你的结论．

拓展延伸
如图4，△ABC中，AG⊥BC于点G，分别以AB、AC为一边向△ABC外作矩形ABME和矩形ACNF，射线GA交EF于点H．若AB=kAE，AC=kAF，试探究HE与HF之间的数量关系，并说明理由．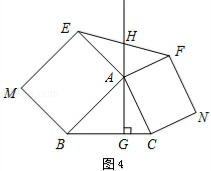

已知，如图所示，在Rt△ABC中，∠C＝90°，有一内接正方形DEFC，连接AF交DE于G，AC＝15，BC＝10，求EG的长．

（本小题满分8分）（1）阅读理解
已知：如图1，△ABC中，AD是中线，点P在AD上，BP、CP的延长线分别交AC、AB于E、F．求证：EF∥BC．

证明：如图2，EF交AD于G,过P作MN∥BC分别交AB、AC于M、N，
在△ABD中，由PM∥BD，得到，同理，
因为BD=CD,所以PM=PN．
在△FBC中，由PM∥BC,所以同理，
，所以△EPF∽△CPB，所以∠FEP=∠PBC，所以EF∥BC．
（2）逆向思考
在△ABC中，D在BC上，点P在AD上，BP、CP的延长线分别交AC、AB于E、F，如果EF∥BC．那么D是BC中点．请你给出证明．
（3）知识应用
①如图3直线a、b、c、d、e、f、g、h是等距的一组平行线，AB在直线g上，请你用无刻度的直尺利用现有平行线作出线段AB的中点．并作简要的画图说明．
②如图4直线a、b、c、d、e、f、g、h是等距的一组平行线，点P不在这些直线上，点A在直线g上，点B在直线c上，请你用无刻度的直尺利用现有平行线作出过点P的直线PQ平行于AB．并作简要的画图说明．

已知：如图，在Rt△ABC中，∠A=90°，以AB为直径作⊙O，BC交⊙O于点D，E是边AC的中点，ED、AB的延长线相交于点F．
求证：（1）DE为⊙O的切线.
（2）AB•DF=AC•BF．

如图，在□ABCD中，过点A作AE⊥BC，垂足为E，连接DE，F为线段DE上一点，且∠AFE=∠B．
（1）求证：△ADF∽△DEC；
（2）若AB=8，AD=6，AF=4，求AE的长．

如图，□ABCD中，E是CD的延长线上一点，BE与AD交于点F，DE=CD。

（1）求证：AB：CE=AF：BC；
（2）若△DEF的面积为3，求：□ABCD的面积。

如图，在正方形ABCD中，E是BC上的一点，连接AE，作BF⊥AE，垂足为H，交CD于F，作CG∥AE，交BF于G．求证：
（1）CG=BH；
（2）FC²=BF•GF；
（3）=．

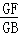如图，四边形ABCD中，AC平分∠DAB，∠ADC=∠ACB=90°，E为AB的中点．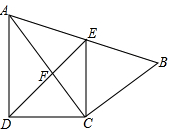

（1）求证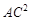：=AB·AD；
（2）若AD=4，AB=6，求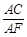的值．

如图1，在△ABC中，∠ACB=90°，经过点B的直线l（l不与直线AB重合）与直线BC的夹角的大小等于∠ABC，分别过点C、A作直线l的垂线，垂足分别为点D、E

（1）写出线段AE、CD之间的数量关系，并加以证明；
（2）当△ABC的位置旋转到图2或图3时，设直线CE、AB交于点F，且，CD=4，请你在图2和图3中任选一种情况，求此时BD的长．

在正方形ABCD中，对角线AC，BD交于点O，点P在线段BC上（不含点B），∠BPE=∠ACB，PE交BO于点E，过点B作BF⊥PE，垂足为F，交AC于点G．
（1）当点P与点C重合时（如图1）．求证：△BOG≌△POE；
（2）结合图2，通过观察、测量、猜想：=______，并证明你的猜想；
（3）把正方形ABCD改为菱形，其他条件不变（如图3），若AC=8，BD=6，直接写出的值．

（满分10分）如图，已知抛物线经过A（-2，0），B（-3，3）及原点O，顶点为C．

（1）求抛物线的解析式；
（2）若点D在抛物线上，点E在抛物线的对称轴上，且A、O、D、E为顶点的四边形是平行四边形，求点D的坐标；
（3）P是抛物线上的第一象限内的动点，过点P作PM⊥x轴，垂足为M，是否存在点P，使得以P、M、A为顶点的三角形△BOC相似？若存在，求出点P的坐标；若不存在，请说明理由．

如图，已知AB是⊙O的直径，直线CD与⊙O相切于点C，AC平分∠DAB．
(1)试说明：AD⊥DC；
(2)若AD＝1，AC＝，求AB的长．

如图，△ABC是等边三角形，⊙O过点B，C，且与BA，CA的延长线分别交于点D，E，弦DF∥AC，EF的延长线交BC的延长线于点G．
（1）求证：△BEF是等边三角形；
（2）若BA=4，CG=2，求BF的长．