初中数学相似多边形的性质解答题

如图，D是△ABC的边AC上的一点，连接BD，已知∠ABD=∠C，AB=6，AD=4，求线段CD的长．

已知a ：b ：c="2" ：3 ：4，且2a＋3b－2c=10，求a， b，c的值。

如图，已知：∠ACB =∠ADC=90°，AD=2，CD=,当AB的长为_____________时，△ACB与△ADC相似．

如图，在Rt△ABC中，∠C＝90º，AB＝10cm，AC∶BC＝4∶3，点P从点A出发沿AB方向向点B运动，速度为1cm/s，同时点Q从点B出发沿B→C→A方向向点A运动，速度为2cm/s，当一个运动点到达终点时，另一个运动点也随之停止运动．

（1）设点P的运动时间为x（秒），△PBQ的面积为y（cm²），当△PBQ存在时，求y与x的函数关系式，并写出自变量x的取值范围；
（2）当x＝5秒时，在直线PQ上是否存在一点M，使△BCM得周长最小，若存在，求出最小周长，若不存在，请说明理由．
（3）当点Q在BC边上运动时，是否存在x，使得以△PBQ的一个顶点为圆心作圆时，另外两个顶点均在这个圆上，若存在，求出 x的值；不存在，说明理由．

如图，在Rt△ABC中，∠C=90°，△ACD沿AD折叠，使得点C落在斜边AB上的点E处．

（1）求证：△BDE∽△BAC；
（2）已知AC=6，BC=8，求线段AD的长度．

如图，每个小方格都是边长为1个单位
的小正方形，A、B、C三点都是格点（每个小方格的顶点叫格点），其中A（1，8），B（3，8），C（4，7）．

（1）若D（2，3），请在网格图中画一个格点△DEF，使△DEF ∽△ABC，且相似比为2∶1；
（2）求△ABC中AC边上的高；
（3）若△ABC外接圆的圆心为P，则点P的坐标为   

在平面直角坐标系中，△ABC的边AB在x轴上，且OA＞OB，以AB为直径的圆与y轴正半轴交于点C，A、B两点的横坐标x_A、x_B是关于x的方程x²＋3x－4=0的两个根．

（1）求点C的坐标；
（2）若∠ACB的平分线所在的直线l交x轴于点D，求直线l对应的一次函数关系式；
（3）过点D任作一直线l′分别交射线CA、CB（点C除外）于点M、N，则＋的值是否为定值？若是，求出定值；若不是，请说明理由．

如图，在矩形ABCD中， CF⊥BD分别交BD、AD于点E、F．

（1）求证：△DEC ∽ △FDC；
（2）若DE＝2，F为AD的中点，求BD的长度．

（1）问题：如图1，在四边形ABCD中，点P为AB上一点，∠DPC=∠A=∠B=90°．求证：AD·BC=AP·BP．
（2）探究：如图2，在四边形ABCD中，点P为AB上一点，当∠DPC=∠A=∠B=θ时，上述结论是否依然成立？说明理由．
（3）应用：请利用（1）（2）获得的经验解决问题：
如图3，在△ABD中，AB=6，AD=BD=5．点P以每秒1个单位长度的速度，由点A 出发，沿边AB向点B运动，且满足∠DPC=∠A．设点P的运动时间为t（秒），当DC的长与△ABD底边上的高相等时，求t的值．

如图，梯形ABCD中，AB//CD，且AB=2CD，E，F分别是AB，BC的中点．
EF与BD相交于点M．

（1）求证：△EDM∽△FBM；
（2）若DB=9，求BM．

为了测量校园水平地面上一棵树的高度，数学兴趣小组利用一根标杆、皮尺，设计如图所示的测量方案．已知测量同学眼睛A、标杆顶端F、树的顶端E在同一直线上，此同学眼睛距地面1．6米，标杆高为3．2米，且BC=2米，CD=6米，求树ED的高．

如图，D是△ABC外一点，E是BC边上一点，∠1=∠2，∠3=∠4．

（1）写出图中两对相似三角形（不得添加字母和线）；
（2）请分别说明两对三角形相似的理由．

如图，∥∥，AB=3，BC=5，DF=12，求DE和EF的长。

已知△ABC，延长BC到D，使CD=BC．取AB的中点F，连接FD交AC于点E．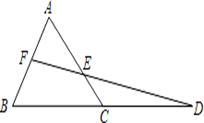

（1）求AE：AC的值；（2）若AB=a，FB=EC，求AC的长．

如图，D是△ABC外一点，E是BC边上一点，∠1=∠2，∠3=∠4．

（1）写出图中两对相似三角形（不得添加字母和线）；
（2）请分别说明两对三角形相似的理由．