(满分14分)如图,已知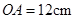 ,
,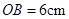 ,点
,点 从点
从点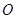 开始沿
开始沿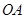 边向点
边向点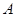 以
以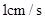 的速度移动,点
的速度移动,点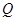 从点
从点 开始向点
开始向点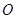 以相同的速度移动,若
以相同的速度移动,若 、
、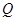 同时出发,移动时间为
同时出发,移动时间为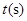 (0≤
(0≤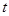 ≤6).
≤6).
(1)设 的面积为
的面积为 ,求
,求 关于
关于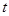 的函数解析式;
的函数解析式;
(2)当 的面积最大时,
的面积最大时, 沿直线
沿直线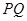 翻折后得到
翻折后得到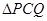 ,试判断点
,试判断点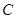 是否落在直线
是否落在直线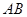 上,并说明理由.
上,并说明理由.
(3)当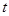 为何值时,
为何值时, 与
与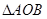 相似.
相似.
(本题14分)在平面直角坐标系中,O为原点,四边形OABC的顶点A在 轴的正半轴上,OA=4,OC=2,点P,点Q分别是边BC,边AB上的点,连结AC,PQ,点B1是点B关于PQ的对称点.
轴的正半轴上,OA=4,OC=2,点P,点Q分别是边BC,边AB上的点,连结AC,PQ,点B1是点B关于PQ的对称点.
(1)若四边形OABC为矩形,如图1,
①求点B的坐标;
②若BQ:BP=1:2,且点B1落在OA上,求点B1的坐标;
(2)若四边形OABC为平行四边形,如图2,且OC⊥AC,过点B1作B1F∥ 轴,与对角线AC、边OC分别交于点E、点F.若B1E: B1F=1:3,点B1的横坐标为
轴,与对角线AC、边OC分别交于点E、点F.若B1E: B1F=1:3,点B1的横坐标为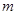 ,求点B1的纵坐标,并直接写出
,求点B1的纵坐标,并直接写出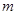 的取值范围.
的取值范围.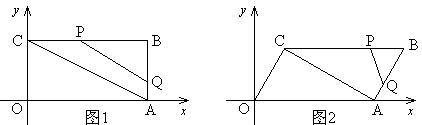
定义:如图1,点M,N把线段AB分割成AM,MN和BN,若以AM,MN,BN为边的三角形是一个直角三角形,则称点M,N是线段AB的勾股分割点
(1)已知点M,N是线段AB的勾股分割点,若AM=2,MN=3求BN的长;
(2)如图2,在△ABC中,FG是中位线,点D,E是线段BC的勾股分割点,且EC>DE≥BD,连接AD,AE分别交FG于点M,N,求证:点M,N是线段FG的勾股分割点
(3)已知点C是线段AB上的一定点,其位置如图3所示,请在BC上画一点D,使C,D是线段AB的勾股分割点(要求尺规作图,保留作图痕迹,画出一种情形即可)
(4)如图4,已知点M,N是线段AB的勾股分割点,MN>AM≥BN,△AMC,△MND和△NBM均是等边三角形,AE分别交CM,DM,DN于点F,G,H,若H是DN的中点,试探究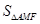 ,
,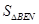 和
和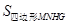 的数量关系,并说明理由
的数量关系,并说明理由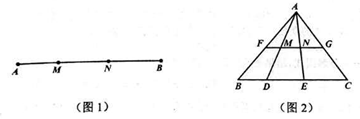
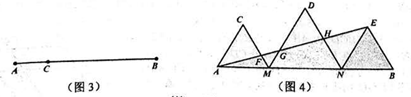
如图,在多边形ABCDE中,∠A=∠AED=∠D=90°,AB=5,AE=2,ED=3,过点E作EF∥CB交AB于点F,FB=1,过AE上的点P作PQ∥AB交线段EF于点O,交折线BCD于点Q,设AP=x,PO.OQ=y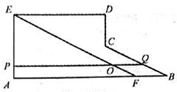
(1)①延长BC交ED于点M,则MD= ,DC=
②求y关于x的函数解析式;
(2)当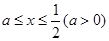 时,
时,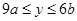 ,求a,b的值;
,求a,b的值;
(3)当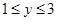 时,请直接写出x的取值范围
时,请直接写出x的取值范围
如图,在Rt△ABC中,∠C=90°,△ACD沿AD折叠,使得点C落在斜边AB上的点E处.
(1)求证:△BDE∽△BAC;
(2)已知AC=6,BC=8,求线段AD的长度.
如图,在△ABC中,D为AC边的中点,且DB⊥BC,BC=4,CD=5.
(1)求DB的长;
(2)在△ABC中,求BC边上高的长.
已知:△ABC是等腰三角形,动点P在斜边AB所在的直线上,以PC为直角边作等腰三角形PCQ,其中∠PCQ=90°,探究并解决下列问题:
(1)如图①,若点P在线段AB上,且AC=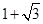 ,PA=
,PA=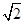 ,则:①线段PB= ,PC= ;
,则:①线段PB= ,PC= ;
②猜想: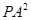 ,
,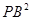 ,
,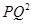 三者之间的数量关系为 ;
三者之间的数量关系为 ;
(2)如图②,若点P在AB的延长线上,在(1)中所猜想的结论仍然成立,请你利用图②给出证明过程;
(3)若动点P满足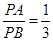 ,求
,求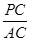 的值.(提示:请利用备用图进行探求)
的值.(提示:请利用备用图进行探求) 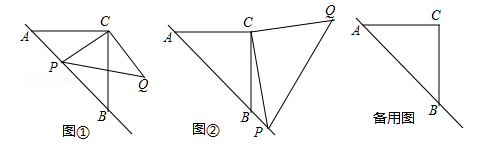
如图,在平面直角坐标系中,点A、C分别在x轴、y轴上,四边形ABCO为矩形,AB=16,点D与点A关于y轴对称,tan∠ACB= ,点E、F分别是线段AD、AC上的动点(点E不与点A、D重合),且∠CEF=∠ACB.
,点E、F分别是线段AD、AC上的动点(点E不与点A、D重合),且∠CEF=∠ACB.
(1)求AC的长和点D的坐标;
(2)说明△AEF与△DCE相似;
(3)当△EFC为等腰三角形时,求点E的坐标.
阅读下面的材料:
小明遇到一个问题:如图1,在□ABCD中,点E是边BC的中点,点F是线段AE上一点,BF的延长线交射线CD于点G.如果 ,求
,求 的值.
的值.
他的做法是:过点E作EH∥AB交BG于点H,那么可以得到△BAF∽△HEF.
请回答:
(1)AB和EH之间的数量关系是 ,CG和EH之间的数量关系是 , 的值为 .
的值为 .
(2)参考小明思考问题的方法,解决问题:
如图2,在四边形ABCD中,DC∥AB,点E是BC延长线上一点,AE和BD相交于点F.如果 ,
, ,求
,求 的值.
的值.
如图,在10×10的正方形网格中,点A,B,C,D均在格点上,以点A为位似中心画四边形AB′C′D′,使它与四边形ABCD位似,且相似比为2.
(1)在图中画出四边形AB′C′D′;
(2)填空:△AC′D′是 三角形.
如图,在△ABC中(BC>AC),∠ACB=90°,点D在AB边上,DE⊥AC于点E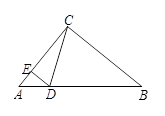
(1)若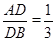 ,AE=2,求EC的长
,AE=2,求EC的长
(2)设点F在线段EC上,点G在射线CB上,以F,C,G为顶点的三角形与△EDC有一个锐角相等,FG交CD于点P,问:线段CP可能是△CFG的高线还是中线?或两者都有可能?请说明理由
如图,已知抛物线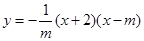 (
(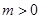 )与x轴相交干点A、B.与y轴相交于点C,且点A在点B的左侧.
)与x轴相交干点A、B.与y轴相交于点C,且点A在点B的左侧.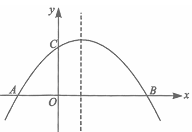
(1)若抛物经过点C(2,2),求实数m的值;
(2)在(1)的条件下,解答下列问题:
①求出△ABC的面积;
②在抛物线的对称轴上找一点H,使AH+CH最小,并求出点H的坐标;
(3)在第四象限内,抛物线上是否存在点M,使得以点A、B、M为顶点的三角形与△ACB相似?若存在,求m的值;若不存在.请说明理由.
如图,在Rt△ABC中,∠ACB=900,AC=6,BC=8.动点M从点A出发,以每秒1个单位长度的速度沿AB向点B匀速运动;同时,动点N从点B出发,以每秒3个单位长度的速度沿BA向点A匀速运动.过线段MN的中点G作边AB的垂线,垂足为点G,交△ABC的另一边于点P,连接PM、PN,当点N运动到点A时,M、N两点同时停止运动,设运动时间为t秒.
(1)当t= 秒时,动点M、N相遇;
(2)设△PMN的面积为S,求S与t之间的函数关系式;
(3)取线段PM的中点K,连接KA、KC,在整个运动过程中,△KAC的面积是否变化?若变化,直接写出它的最大值和最小值;若不变化,请说明理由.
设ω是一个平面图形,如果用直尺和圆规经过有限步作图(简称尺规作图),画出一个正方形与ω的面积相等(简称等积),那么这样的等积转化称为ω的“化方”.
(1)阅读填空
如图①,已知矩形ABCD,延长AD到E,使DE=DC,以AE为直径作半圆.延长CD交半圆于点H,以DH为边作正方形DFGH,则正方形DFGH与矩形ABCD等积.
理由:连接AH,EH.
∵AE为直径,∴∠AHE=90°,∴∠HAE+∠HEA=90°.
∵DH⊥AE,∴∠ADH=∠EDH=90°
∴∠HAD+∠AHD=90°
∴∠AHD=∠HED,∴△ADH∽ .
∴ ,即DH2=AD×DE.
,即DH2=AD×DE.
又∵DE=DC
∴DH2= ,即正方形DFGH与矩形ABCD等积.
(2)操作实践
平行四边形的“化方”思路是,先把平行四边形转化为等积的矩形,再把矩形转化为等积的正方形.
如图②,请用尺规作图作出与▱ABCD等积的矩形(不要求写具体作法,保留作图痕迹).
(3)解决问题三角形的“化方”思路是:先把三角形转化为等积的 (填写图形名称),再转化为等积的正方形.
如图③,△ABC的顶点在正方形网格的格点上,请作出与△ABC等积的正方形的一条边(不要求写具体作法,保留作图痕迹,不通过计算△ABC面积作图).
(4)拓展探究
n边形(n>3)的“化方”思路之一是:把n边形转化为等积的n﹣1边形,…,直至转化为等积的三角形,从而可以化方.
如图④,四边形ABCD的顶点在正方形网格的格点上,请作出与四边形ABCD等积的三角形(不要求写具体作法,保留作图痕迹,不通过计算四边形ABCD面积作图).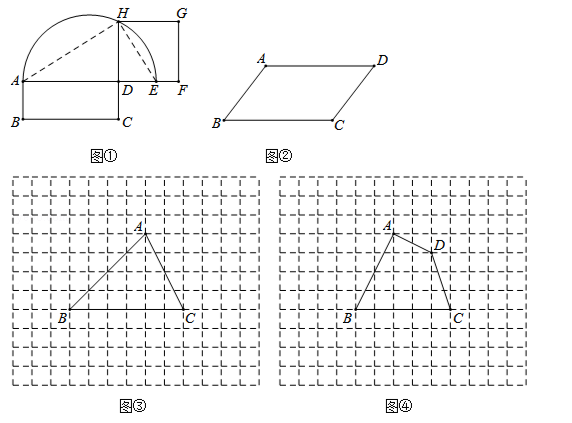
试题篮
()