初中数学相似多边形的性质填空题

在某一时刻，测得一根高为1.8m的竹竿的影长为3m，同时测得一根旗杆的影长为25m，那么这根旗杆的高度为   m．  

设点O为投影中心，长度为1的线段AB平行于它在面H内的投影，投影的长度为3，且O到直线AB的距离为1.5，那么直线AB与直线的距离为_______．

如上图，△ABC中，D，E分别是AB，AC上的点（DE≠BC），当       或       或       时，△ADE∽△ACB相似．

把一矩形纸片对折，如果对折后的矩形与原矩形相似，则原矩形纸片的长与宽之比为       ．

如图，在菱形ABCD中，点M在对角线AC上，AM＝3，ME⊥AB于E，ME＝1．P是MC上的一个动点，PF⊥AD于F．若设MP＝x，PF＝y，则y与x的函数关系式为    ．

如图，将矩形纸片ABCD(AD>DC)的一角沿着过点D的直线折叠，使点A与BC边上的点E重合，折痕交AB于点F.若BE:EC=1:2，则AF:FB=           

如图，等腰直角三角形ABC的顶点A，C在x轴上，∠ACB=90°，AC=BC=，反比例函数（）的图象分别与AB，BC交于点D，E．连接DE，当△BDE∽△BCA时，点E的坐标为______________．

如图，在△ABC中，AB=AC=10，点D是边BC上一动点（不与B，C重合），∠ADE=∠B=α，DE交AC于点E，且cosα=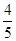．下列结论：
①△ADE∽△ACD；
②当BD=6时，△ABD与△DCE全等；
③△DCE为直角三角形时，BD为8或；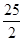
④0＜CE≤6.4．
其中正确的结论是_________ ．（把你认为正确结论的序号都填上）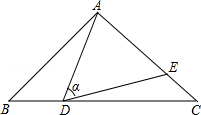

如图，等腰直角三角形ABC的顶点A，C在x轴上，∠ACB=90°，，反比例
函数（）的图象分别与AB，BC交于点D，E．连接DE，当△BDE∽△BCA时，点E的坐标为______________．

已知：△ABC在直角坐标平面内，三个顶点的坐标分别为A（0，3）、B（3，4）、C（2，2）（正方形网格中每个小正方形的边长是一个单位长度）．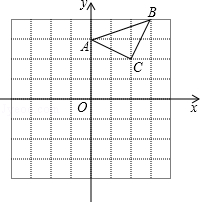

（1）画出△ABC向下平移4个单位长度得到的△A₁B₁C₁，点C₁的坐标是_________ ；
（2）以点B为位似中心，在网格内画出△A₂B₂C₂，使△A₂B₂C₂与△ABC位似，且位似比为2：1，点C₂的坐标是_________ ；
（3）△A₂B₂C₂的面积是_________ 平方单位．

如图，在△ABC中，AB=AC=10，点D是边BC上一动点（不与B，C重合），∠ADE=∠B=α，DE交AC于点E，且cosα=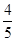．下列结论：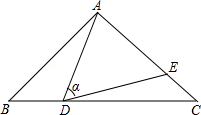

①△ADE∽△ACD；
②当BD=6时，△ABD与△DCE全等；
③△DCE为直角三角形时，BD为8或；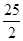
④0＜CE≤6.4．
其中正确的结论是_________ ．（把你认为正确结论的序号都填上）

已知：△ABC在直角坐标平面内，三个顶点的坐标分别为A（0，3）B（3，4）C（2，2）（正方形网格中每个小正方形的边长是一个单位长度）．

（1）在网格内画出△ABC向下平移4个单位长度得到的，并写出点的坐标是       ；
（2）以点B为位似中心，在网格内画出，使与△ABC位似，且位似比为2︰1，并写出点的坐标是       ；
（3）的面积是       平方单位．

如图，直线∥∥，，，那么的值是       .

如果两个相似三角形的对应中线之比是1︰4，那么它们的周长比是       .

如图，已知分别是△的边和上的点，，，要使∥，
那么应等于      ；