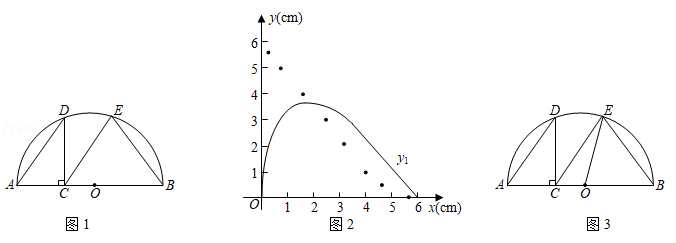
如图1,点 是半圆 的直径 上一动点(不包括端点), ,过点 作 交半圆于点 ,连结 ,过点 作 交半圆于点 ,连结 .牛牛想探究在点 运动过程中 与 的大小关系.他根据学习函数的经验,记 , , .请你一起参与探究函数 、 随自变量 变化的规律.
通过几何画板取点、画图、测量,得出如下几组对应值,并在图2中描出了以各对对应值为坐标的点,画出了不完整图象.
|
|
|
0.30 |
0.80 |
1.60 |
2.40 |
3.20 |
4.00 |
4.80 |
5.60 |
|
|
|
|
2.01 |
2.98 |
3.46 |
3.33 |
2.83 |
2.11 |
1.27 |
0.38 |
|
|
|
|
5.60 |
4.95 |
3.95 |
2.96 |
2.06 |
1.24 |
0.57 |
0.10 |
|
(1)当 时, .
(2)在图2中画出函数 的图象,并结合图象判断函数值 与 的大小关系.
(3)由(2)知" 取某值时,有 ".如图3,牛牛连结了 ,尝试通过计算 , 的长来验证这一结论,请你完成计算过程.
【证明体验】
(1)如图1, 为 的角平分线, ,点 在 上, .求证: 平分 .
【思考探究】
(2)如图2,在(1)的条件下, 为 上一点,连结 交 于点 .若 , , ,求 的长.
【拓展延伸】
(3)如图3,在四边形 中,对角线 平分 , ,点 在 上, .若 , , ,求 的长.

如图,锐角三角形 内接于 , 的平分线 交 于点 ,交 边于点 ,连接 .
(1)求证: .
(2)已知 , ,求线段 的长(用含 , 的代数式表示).
(3)已知点 在线段 上(不与点 ,点 重合),点 在线段 上(不与点 ,点 重合), ,求证: .

如图, 是 的直径,点 是 上异于 、 的点,连接 、 ,点 在 的延长线上,且 ,点 在 的延长线上,且 .
(1)求证: 是 的切线;
(2)若 , ,求 的长.

如图,点 在以 为直径的 上,过 作 的切线交 延长线于点 , 于点 ,交 于点 ,连接 , .
(1)求证: ;
(2)求证: ;
(3)若 , ,求 的长.

如图1,在四边形 中, ,点 在边 上,且 , ,作 交线段 于点 ,连接 .
(1)求证: ;
(2)如图2.若 , , ,求 的长;
(3)如图3,若 的延长线经过 的中点 ,求 的值.

如图1, 为 上一点,点 在直径 的延长线上,且 .
(1)判断直线 与 的位置关系,并说明理由;
(2)若 , ,求 的半径;
(3)如图2,在(2)的条件下, 的平分线 交 于点 ,交 于点 ,连结 .求 的值.

如图,点 在正方形 边 上,点 是线段 上的动点(不与点 重合), 交 于点 , 于点 , , .
(1)求 ;
(2)设 , ,试探究 与 的函数关系式(写出 的取值范围);
(3)当 时,判断 与 的位置关系并说明理由.
如图, 是 的内接三角形,过点 作 的切线交 的延长线于点 , 是 的直径,连接 .
(1)求证: ;
(2)若 , 于点 , , ,求 的值.

如图,在 中, , 平分 交 于点 ,点 在 上, , 是 的外接圆,交 于点 .
(1)求证: 是 的切线;
(2)若 的半径为5, ,求 .

在等腰 中, ,点 是 边上一点(不与点 、 重合),连结 .
(1)如图1,若 ,点 关于直线 的对称点为点 ,连结 , ,则 ;
(2)若 ,将线段 绕点 顺时针旋转 得到线段 ,连结 .
①在图2中补全图形;
②探究 与 的数量关系,并证明;
(3)如图3,若 ,且 .试探究 、 、 之间满足的数量关系,并证明.

如图1,在 中, , ,点 是 边上一点(含端点 、 ,过点 作 垂直于射线 ,垂足为 ,点 在射线 上,且 ,连接 、 .

(1)求证: ;
(2)如图2,连接 ,点 、 、 分别为线段 、 、 的中点,连接 、 、 .求 的度数及 的值;
(3)在(2)的条件下,若 ,直接写出 面积的最大值.
如图, AB是⊙ O的直径,点 F在⊙ O上,∠ BAF的平分线 AE交⊙ O于点 E,过点 E作 ,交 AF的延长线于点 D,延长 DE、 AB相交于点 C.
(1)求证: CD是⊙ O的切线;
(2)若⊙ O的半径为5, ,求 BC的长.

某数学兴趣小组在数学课外活动中,对多边形内两条互相垂直的线段做了如下探究: 
【观察与猜想】
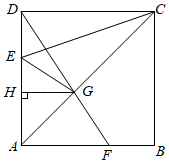
(1)如图1,在正方形 中,点 , 分别是 , 上的两点,连接 , , ,则 的值为 ;
(2)如图2,在矩形 中, , ,点 是 上的一点,连接 , ,且 ,则 的值为 ;
【类比探究】
(3)如图3,在四边形 中, ,点 为 上一点,连接 ,过点 作 的垂线交 的延长线于点 ,交 的延长线于点 ,求证: ;

【拓展延伸】
(4)如图4,在 中, , , ,将 沿 翻折,点 落在点 处得 ,点 , 分别在边 , 上,连接 , , .
①求 的值;
②连接 ,若 ,写出 的长度.
试题篮
()