初中数学解直角三角形填空题

点A,B,C都在半径为r的圆上，直线AD⊥直线BC，垂足为D，直线BE⊥直线AC，垂足为E，直线AD与BE相交于点H，若，则∠ABC所对的弧长等于       （长度单位）.

如图，在边长为2的菱形ABCD中，∠A=60°，M是AD边的中点，N是AB边上一动点，将△AMN沿MN所在的直线翻折得到△A′MN，连接A′C. 则A′C长度的最小值是       .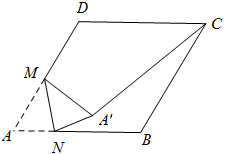

如图（1），有两个全等的正三角形ABC和ODE，点O、C分别为△ABC、△DEO的重心；固定点O，将△ODE顺时针旋转，使得OD经过点C，如图（2）所示，则图（2）中四边形OGCF与△OCH面积的比为           .

如图，菱形ABCD中，AB=4，∠ABC=60°，点P，Q，K分别为线段BC，CD，BD上的任意一点，则PK+QK的最小值为           .

如图，、分别切⊙于点、，点是⊙上一点，且，则       度；若PA＝4，则AO＝       ．

如图所示中的∠A的正切值为   ．

如图，已知直线y=x+4与两坐标轴分别交于A、B两点，⊙C的圆心坐标为 （2，O），半径为2，若D是⊙C上的一个动点，线段DA与y轴交于点E，则△ABE面积的最小值和最大值分别是　    　．

如图，已知⊙O的直径AB=6，E、F为AB的三等分点，M、N为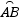上两点，且∠MEB=∠NFB=60°，则EM+FN=　　．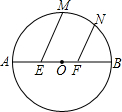

如图，在△ABC中，AB=AC，BC=8，tanC=，如果将△ABC沿直线l翻折后，点B落在边AC的中点处，直线l与边BC交于点D，那么BD的长为　　．

如图，△ABC是边长为1的等边三角形．取BC边中点E，作ED∥AB，EF∥AC，得到四边形EDAF，它的面积记作S₁；取BE中点E₁，作E₁D₁∥FB，E₁F₁∥EF，得到四边形E₁D₁FF₁，它的面积记作S₂．照此规律作下去，则S₂₀₁₄=                   .

已知梯形ABCD中，AD∥BC，AB=15，CD=13，AD=8，∠B是锐角，∠B的正弦值为，那么BC的长为       ．

在中，，，，以AB为一边作等腰直角三角形ABD，使，连结CD，则线段CD的长为__________.

如图，点G是Rt△ABC的重心，过点G作矩形GECF，当GF：GE=1：2时，则∠ B的正切值为   ．

如图，在平行四边形ABCD中，AD＝5cm， AP＝8cm， AP平分∠DAB，交DC于点P，过点B作BE⊥AD于点E，BE交AP于点F，则tan∠BFP＝        ．

如图，直径为10的⊙A经过点C(0,5)和点O (0,0)，B是y轴右侧⊙A优弧上一点,则∠OBC 的正弦值为                ．