初中数学解直角三角形的应用试题

如图，池塘边一棵垂直于水面 $\mathit{BM}$的笔直大树 $\mathit{AB}$在点 $C$处折断， $\mathit{AC}$部分倒下，点 $A$与水面上的点 $E$重合，部分沉入水中后，点 $A$与水中的点 $F$重合， $\mathit{CF}$交水面于点 $D$， $\mathit{DF}=2m$， $\angle \mathit{CEB}=30°$， $\angle \mathit{CDB}=45°$，求 $\mathit{CB}$部分的高度．（精确到 $0.1m$．参考数据： $\sqrt{2}\approx 1.41$， $\sqrt{3}\approx 1.73)$

如图，河的两岸 $a$， $b$互相平行，点 $A$， $B$， $C$是河岸 $b$上的三点，点 $P$是河岸 $a$上的一个建筑物，某人在河岸 $b$上的 $A$处测得 $\angle \mathit{PAB}=30°$，在 $B$处测得 $\angle \mathit{PBC}=75°$，若 $\mathit{AB}=80$米，则河两岸之间的距离约为　　米． $(\sqrt{3}\approx 1.73$，结果精确到0.1米）

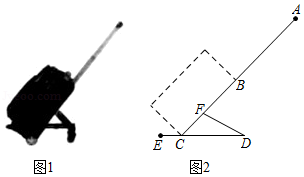
小李要外出参加“建国70周年”庆祝活动，需网购一个拉杆箱，图①，②分别是她上网时看到的某种型号拉杆箱的实物图与示意图，并获得了如下信息：滑杆 $\mathit{DE}$，箱长 $\mathit{BC}$，拉杆 $\mathit{AB}$的长度都相等，即 $\mathit{DE}=\mathit{BC}=\mathit{AB}$， $B$， $F$在 $\mathit{AC}$上， $C$在 $\mathit{DE}$上，支杆 $\mathit{DF}=30\mathit{cm}$， $\mathit{CE}:\mathit{CD}=1:3$， $\angle \mathit{DCF}=45°$， $\angle \mathit{CDF}=30°$，请根据以上信息，解决下列问题．

（1）求 $\mathit{AC}$的长度（结果保留根号）；

（2）求拉杆端点 $A$到水平滑杆 $\mathit{ED}$的距离（结果保留根号）．

两栋居民楼之间的距离 $\mathit{CD}=30$米，楼 $\mathit{AC}$和 $\mathit{BD}$均为10层，每层楼高3米．

（1）上午某时刻，太阳光线 $\mathit{GB}$与水平面的夹角为 $30°$，此刻 $B$楼的影子落在 $A$楼的第几层？

（2）当太阳光线与水平面的夹角为多少度时， $B$楼的影子刚好落在 $A$楼的底部？

为加快城乡对接，建设全域美丽乡村，某地区对 $A$、 $B$两地间的公路进行改建．如图， $A$、 $B$两地之间有一座山，汽车原来从 $A$地到 $B$地需途经 $C$地沿折线 $\mathit{ACB}$行驶，现开通隧道后，汽车可直接沿直线 $\mathit{AB}$行驶．已知 $\mathit{BC}=80$千米， $\angle A=45°$， $\angle B=30°$．

（1）开通隧道前，汽车从 $A$地到 $B$地大约要走多少千米？

（2）开通隧道后，汽车从 $A$地到 $B$地大约可以少走多少千米？（结果精确到0.1千米）（参考数据： $\sqrt{2}\approx 1.41$， $\sqrt{3}\approx 1.73)$

图1是某小区入口实景图，图2是该入口抽象成的平面示意图．已知入口 $\mathit{BC}$宽3.9米，门卫室外墙 $\mathit{AB}$上的 $O$点处装有一盏路灯，点 $O$与地面 $\mathit{BC}$的距离为3.3米，灯臂 $\mathit{OM}$长为1.2米（灯罩长度忽略不计）， $\angle \mathit{AOM}=60°$．

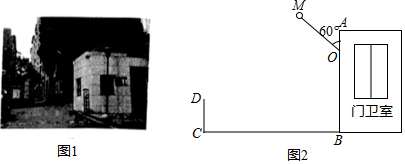
（1）求点 $M$到地面的距离；

（2）某搬家公司一辆总宽2.55米，总高3.5米的货车从该入口进入时，货车需与护栏 $\mathit{CD}$保持0.65米的安全距离，此时，货车能否安全通过？若能，请通过计算说明；若不能，请说明理由．（参考数据： $\sqrt{3}\approx 1.73$，结果精确到0.01米）

图1是一商场的推拉门，已知门的宽度 $\mathit{AD}=2$米，且两扇门的大小相同（即 $\mathit{AB}=\mathit{CD})$，将左边的门 $\mathit{AB}{B}_1{A}_1$绕门轴 $A{A}_1$向里面旋转 $37°$，将右边的门 $\mathit{CD}{D}_1{C}_1$绕门轴 $D{D}_1$向外面旋转 $45°$，其示意图如图2，求此时 $B$与 $C$之间的距离（结果保留一位小数）．（参考数据： $\sin 37°\approx 0.6$， $\cos 37°\approx 0.8$， $\sqrt{2}\approx 1.4)$

位于张家界核心景区的贺龙铜像，是我国近百年来最大的铜像．铜像由像体 $\mathit{AD}$和底座 $\mathit{CD}$两部分组成．如图，在 $\text{Rt}\Delta \text{ABC}$中， $\angle \mathit{ABC}=70.5°$，在 $\text{Rt}\Delta \text{DBC}$中， $\angle \mathit{DBC}=45°$，且 $\mathit{CD}=2.3$米，求像体 $\mathit{AD}$的高度（最后结果精确到0.1米，参考数据： $\sin 70.5°\approx 0.943$， $\cos 70.5°\approx 0.334$， $\tan 70.5°\approx 2.824)$

问题背景：已知 $\angle \mathit{EDF}$的顶点 $D$在 $\mathit{\Delta ABC}$的边 $\mathit{AB}$所在直线上（不与 $A$， $B$重合）， $\mathit{DE}$交 $\mathit{AC}$所在直线于点 $M$， $\mathit{DF}$交 $\mathit{BC}$所在直线于点 $N$，记 $\mathit{\Delta ADM}$的面积为 $S_1$， $\mathit{\Delta BND}$的面积为 $S_2$．

（1）初步尝试：如图①，当 $\mathit{\Delta ABC}$是等边三角形， $\mathit{AB}=6$， $\angle \mathit{EDF}=\angle A$，且 $\mathit{DE}//\mathit{BC}$， $\mathit{AD}=2$时，则 $S_1·S_2=$　　；

（2）类比探究：在（1）的条件下，先将点 $D$沿 $\mathit{AB}$平移，使 $\mathit{AD}=4$，再将 $\angle \mathit{EDF}$绕点 $D$旋转至如图②所示位置，求 $S_1·S_2$的值；

（3）延伸拓展：当 $\mathit{\Delta ABC}$是等腰三角形时，设 $\angle B=\angle A=\angle \mathit{EDF}=\alpha$．

（Ⅰ）如图③，当点 $D$在线段 $\mathit{AB}$上运动时，设 $\mathit{AD}=a$， $\mathit{BD}=b$，求 $S_1·S_2$的表达式（结果用 $a$， $b$和 $\alpha$的三角函数表示）．

（Ⅱ）如图④，当点 $D$在 $\mathit{BA}$的延长线上运动时，设 $\mathit{AD}=a$， $\mathit{BD}=b$，直接写出 $S_1·S_2$的表达式，不必写出解答过程．

某太阳能热水器的横截面示意图如图所示，已知真空热水管 $\mathit{AB}$与支架 $\mathit{CD}$所在直线相交于点 $O$，且 $\mathit{OB}=\mathit{OD}$，支架 $\mathit{CD}$与水平线 $\mathit{AE}$垂直， $\angle \mathit{BAC}=\angle \mathit{CDE}=30°$， $\mathit{DE}=80\mathit{cm}$， $\mathit{AC}=165\mathit{cm}$．

（1）求支架 $\mathit{CD}$的长；

（2）求真空热水管 $\mathit{AB}$的长．（结果保留根号）

如图，电线杆 $\mathit{CD}$的高度为 $h$，两根拉线 $\mathit{AC}$与 $\mathit{BC}$相互垂直， $\angle \mathit{CAB}=\alpha$，则拉线 $\mathit{BC}$的长度为 $(A$、 $D$、 $B$在同一条直线上） $($　　 $)$

A． $\frac{h}{\sin \alpha }$B． $\frac{h}{\cos \alpha }$C． $\frac{h}{\tan \alpha }$D． $h\cdot \cos \alpha$

某游乐场部分平面图如图所示， $C$、 $E$、 $A$在同一直线上， $D$、 $E$、 $B$在同一直线上，测得 $A$处与 $E$处的距离为80 米， $C$处与 $D$处的距离为34米， $\angle C=90°$， $\angle \mathit{ABE}=90°$， $\angle \mathit{BAE}=30°$． $(\sqrt{2}\approx 1.4$， $\sqrt{3}\approx 1.7)$

（1）求旋转木马 $E$处到出口 $B$处的距离；

（2）求海洋球 $D$处到出口 $B$处的距离（结果保留整数）．

如图1，2分别是某款篮球架的实物图与示意图，已知底座 $\mathit{BC}=0.60$米，底座 $\mathit{BC}$与支架 $\mathit{AC}$所成的角 $\angle \mathit{ACB}=75°$，支架 $\mathit{AF}$的长为2.50米，篮板顶端 $F$点到篮筐 $D$的距离 $\mathit{FD}=1.35$米，篮板底部支架 $\mathit{HE}$与支架 $\mathit{AF}$所成的角 $\angle \mathit{FHE}=60°$，求篮筐 $D$到地面的距离（精确到0.01米）（参考数据： $\cos 75°\approx 0.2588$， $\sin 75°\approx 0.9659$， $\tan 75°\approx 3.732$， $\sqrt{3}\approx 1.732$， $\sqrt{2}\approx 1.414)$

某国发生8.1级强烈地震，我国积极组织抢险队赴地震灾区参与抢险工作，如图，某探测队在地面 $A$、 $B$两处均探测出建筑物下方 $C$处有生命迹象，已知探测线与地面的夹角分别是 $25°$和 $60°$，且 $\mathit{AB}=4$米，求该生命迹象所在位置 $C$的深度．（结果精确到1米，参考数据： $\sin 25°\approx 0.4$， $\cos 25°\approx 0.9$， $\tan 25°\approx 0.5$， $\sqrt{3}\approx 1.7)$

如图，吊车在水平地面上吊起货物时，吊绳 $\mathit{BC}$与地面保持垂直，吊臂 $\mathit{AB}$与水平线的夹角为 $64°$，吊臂底部 $A$距地面 $1.5m$．（计算结果精确到 $0.1m$，参考数据 $\sin 64°\approx 0.90$， $\cos 64°\approx 0.44$， $\tan 64°\approx 2.05)$

（1）当吊臂底部 $A$与货物的水平距离 $\mathit{AC}$为 $5m$时，吊臂 $\mathit{AB}$的长为　　 $m$．

（2）如果该吊车吊臂的最大长度 $\mathit{AD}$为 $20m$，那么从地面上吊起货物的最大高度是多少？（吊钩的长度与货物的高度忽略不计）