初中数学解直角三角形的应用试题

美丽的黄河宛如一条玉带穿城而过，沿河两岸的滨河路风情线是兰州最美的景观之一．数学课外实践活动中，小林在南滨河路上的A，B两点处，利用测角仪分别对北岸的一观景亭D进行了测量．如图，测得∠DAC＝45°，∠DBC＝65°．若AB＝132米，求观景亭D到南滨河路AC的距离约为多少米？（结果精确到1米，参考数据：sin65°≈0.91，cos65°≈0.42，tan65°≈2.14）

“兰州中山桥“位于兰州滨河路中段白塔山下、金城关前，是黄河上第一座真正意义上的桥梁，有“天下黄河第一桥“之美誉．它像一部史诗，记载着兰州古往今来历史的变迁．桥上飞架了5座等高的弧形钢架拱桥．

小芸和小刚分别在桥面上的A，B两处，准备测量其中一座弧形钢架拱梁顶部C处到桥面的距离．已知AB＝20m，小芸在A处测得∠CAB＝36°，小刚在B处测得∠CBA＝43°，求弧形钢架拱梁顶部C处到桥面的距离．（结果精确到0.1m）（参考数据sin36°≈0.59，cos36°≈0.81，tan36°≈0.73，sin43°≈0.68，cos43°≈0.73，tan43°≈0.93）

如图，旗杆高 AB＝8 m，某一时刻，旗杆影子长 BC＝16 m，则tan C＝ 　　．

两栋居民楼之间的距离 CD＝30 m，楼 AC和 BD均为10层，每层楼高为3 m．上午某时刻，太阳光线 GB与水平面的夹角为30°，此刻楼 BD的影子会遮挡到楼 AC的第几层？（参考数据： $\sqrt{3}$ ≈1.7， $\sqrt{2}$ ≈1.4）

如图，一根竖直的木杆在离地面3.1 m处折断，木杆顶端落在地面上，且与地面成38°角，则木杆折断之前高度约为 　　 m．

（参考数据：sin38°≈0.62，cos38°≈0.79，tan38°≈0.78）

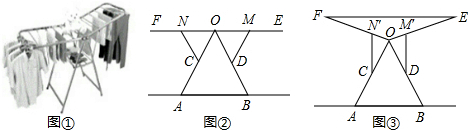
王阿姨家的阳台上放置了一个晾衣架，完全稳固张开如图①．图②，③是晾衣架的侧面展开图，△ AOB是边长为130 cm的等边三角形，晾衣架 OE， OF能以 O为圆心转动，且 OE＝ OF＝130 cm：在 OA， OB上的点 C， D处分别有支撑杆 CN， DM能以 C， D为圆心转动．

（1）如图②，若 EF平行于地面 AB，王阿姨的衣服穿在衣架上的总长度是110 cm，垂挂在晾衣杆 OE上是否会拖到地面上？说明理由．

（2）如图③，当支撑杆 DM支到点 M′，此时∠ EOB＝78°，点 E离地面距离最大．保证衣服不拖到地面上，衣服穿在衣架上的总长度最长约为多少厘米？（结果取整）参考数据：（ $\sqrt{\text{3}}\approx \frac{\text{17}}{\text{10}}$ ，sin78°≈ $\frac{\text{49}}{\text{50}}$ ，cos78°≈ $\frac{\text{1}}{\text{5}}$ ，sin18°≈ $\frac{\text{3}}{\text{10}}$ ，cos18°≈ $\frac{\text{19}}{\text{20}}$ ）

“一号龙卷风”给小岛O造成了较大的破坏，救灾部门迅速组织力量，从仓储D处调集救援物资，计划先用汽车运到与D在同一直线上的C、B、A三个码头中的一处，再用货船运到小岛O．已知：OA⊥AD，∠ODA＝15°，∠OCA＝30°，∠OBA＝45°，CD＝20km．若汽车行驶的速度为50km/时，货船航行的速度为25km/时，问这批物资在哪个码头装船，最早运抵小岛O？（在物资搬运能力上每个码头工作效率相同，参考数据： $\sqrt{2}\approx 1.4,\sqrt{3}\approx 1.7$）．

如图，校园内有一棵与地面垂直的树，数学兴趣小组两次测量它在地面上的影子，第一次是阳光与地面成60°角时，第二次是阳光与地面成30°角时，两次测量的影长相差8米，则树高　　米．（结果保留根号）

如图，地面上小山的两侧有 A， B两地，为了测量 A， B两地的距离，让一热气球从小山西侧 A地出发沿与 AB成30°角的方向，以每分钟40 m的速度直线飞行，10分钟后到达 C处，此时热气球上的人测得 CB与 AB成70°角，请你用测得的数据求 A， B两地的距离 AB长．（结果用含非特殊角的三角函数和根式表示即可）

如图1，在△ ABC中，设∠ A、∠ B、∠ C的对边分别为 a， b， c，过点 A作 AD⊥ BC，垂足为 D，会有sin∠ C＝ $\frac{\mathit{AD}}{\mathit{AC}}$ ，则

S _{△ ABC}＝ $\frac{1}{2}$ BC× AD＝ $\frac{1}{2}$ × BC× ACsin∠ C＝ $\frac{1}{2}$ absin∠ C，

即 S _{△ ABC}＝ $\frac{1}{2}$ absin∠ C

同理 S _{△ ABC}＝ $\frac{1}{2}$ bcsin∠ A

S _{△ ABC}＝ $\frac{1}{2}$ acsin∠ B

通过推理还可以得到另一个表达三角形边角关系的定理﹣余弦定理：

如图2，在△ ABC中，若∠ A、∠ B、∠ C的对边分别为 a， b， c，则

a ²＝ b ²+ c ²﹣2 bccos∠ A

b ²＝ a ²+ c ²﹣2 accos∠ B

c ²＝ a ²+ b ²﹣2 abcos∠ C

用上面的三角形面积公式和余弦定理解决问题：

（1）如图3，在△ DEF中，∠ F＝60°，∠ D、∠ E的对边分别是3和8．求 S _{△ DEF}和 DE ²．

解： S _{△ DEF}＝ EF× DFsin∠ F＝ 　　；

DE ²＝ EF ²+ DF ²﹣2 EF× DFcos∠ F＝ 　　．

（2）如图4，在△ ABC中，已知 AC＞ BC，∠ C＝60°，△ ABC'、△ BCA'、△ ACB'分别是以 AB、 BC、 AC为边长的等边三角形，设△ ABC、△ ABC'、△ BCA'、△ ACB'的面积分别为 S ₁、 S ₂、 S ₃、 S ₄，求证： S ₁+ S ₂＝ S ₃+ S ₄．

王浩同学用木板制作一个带有卡槽的三角形手机架，如图所示．已知 AC＝20 cm， BC＝18 cm，∠ ACB＝50°，王浩的手机长度为17 cm，宽为8 cm，王浩同学能否将手机放入卡槽 AB内？请说明你的理由．（提示：sin50°≈0.8，cos50°≈0.6，tan50°≈1.2）

如图，以边长为20cm的正三角形铁皮的各顶点为端点，在各边上分别截取6cm长的六条线段，过截得的六个端点作所在边的垂线，形成三个有两个直角的四边形．把它们沿虚线剪掉，用剩下的纸板折成一个底为正三角形的无盖柱形盒子，则这个盒子的容积为　　cm³．

图1是安装在倾斜屋顶上的热水器，图2是安装热水器的侧面示意图．已知屋面 AE的倾斜角∠ EAD为22°，长为2米的真空管 AB与水平线 AD的夹角为37°，安装热水器的铁架竖直管 CE的长度为0.5米．

（1）真空管上端 B到水平线 AD的距离．

（2）求安装热水器的铁架水平横管 BC的长度（结果精确到0.1米）．

（参考数据： $\sin {37}^{\circ }\approx \frac{3}{5}$ ， $\cos {37}^{\circ }\approx \frac{4}{5}$ ， $\tan {37}^{\circ }\approx \frac{3}{4}$ ， $\sin {22}^{\circ }\approx \frac{3}{8}$ ， $\cos {22}^{\circ }\approx \frac{15}{16}$ ， $\tan {22}^{\circ }\approx \frac{2}{5}$ ）

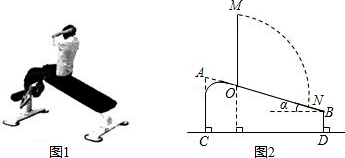
图①是小明在健身器材上进行仰卧起坐锻炼时的情景，图②是小明锻炼时上半身由ON位置运动到与地面垂直的OM位置时的示意图．已知AC＝0.66米，BD＝0.26米，α＝20°．（参考数据：sin20°≈0.342，cos20°≈0.940，tan20°≈0.364）

（1）求AB的长（精确到0.01米）；

（2）若测得ON＝0.8米，试计算小明头顶由N点运动到M点的路径 $\stackrel{̂}{\mathit{MN}}$的长度．（结果保留π）

如图，一垂直于地面的灯柱AB被一钢线CD固定，CD与地面成45°夹角（∠CDB＝45°），在C点上方2米处加固另一条钢线ED，ED与地面成53°夹角（∠EDB＝53°），那么钢线ED的长度约为多少米？（结果精确到1米，参考数据：sin53°≈0.80，cos53°≈0.60，tan53°≈1.33）