初中数学解直角三角形的应用试题

鲁南高铁临沂段修建过程中需要经过一座小山．如图，施工方计划沿方向开挖隧道，为了加快施工速度，要在小山的另一侧、、共线）处同时施工．测得，，，求的长．

图1是一种折叠式晾衣架．晾衣时，该晾衣架左右晾衣臂张开后示意图如图2所示，两支脚分米，展开角，晾衣臂分米，晾衣臂支架分米，且分米．当时，点离地面的距离为　　        ；分米，当从水平状态旋转到（在延长线上）时，点绕点随之旋转至上的点处，则为　　分米．

如图，一架长为6米的梯子斜靠在一竖直的墙上，这时测得，如果梯子的底端外移到，则梯子顶端下移到，这时又测得，那么的长度约为　米．，，，

如图1，一种折叠式小刀由刀片和刀鞘两部分组成．现将小刀打开成如图2位置，刀片部分是四边形 $\mathit{ABCD}$，其中 $\mathit{AD}//\mathit{BC}$， $\mathit{AB}\perp \mathit{BC}$， $\mathit{CD}=15\mathit{mm}$， $\angle C=53°$，刀鞘的边缘 $\mathit{MN}//\mathit{PQ}$，刀刃 $\mathit{BC}$与刀鞘边缘 $\mathit{PQ}$相交于点 $O$，点 $A$恰好落在刀鞘另一边缘 $\mathit{MN}$上时， $\angle \mathit{COP}=37°$， $\mathit{OC}=50\mathit{mm}$，

（1）求刀片宽度 $h$．

（2）若刀鞘宽度为 $14\mathit{mm}$，求刀刃 $\mathit{BC}$的长度．（结果精确到 $0.1\mathit{mm})$（参考数据： $\sin 37°\approx \frac{3}{5}$， $\cos 37°\approx \frac{4}{5}$， $\tan 37°\approx \frac{3}{4})$

如图，在岷江的右岸边有一高楼，左岸边有一坡度的山坡，点与点在同一水平面上，与在同一平面内．某数学兴趣小组为了测量楼的高度，在坡底处测得楼顶的仰角为，然后沿坡面上行了米到达点处，此时在处测得楼顶的仰角为，求楼的高度．

有一种升降熨烫台如图1所示，其原理是通过改变两根支撑杆夹角的度数来调整熨烫台的高度．图2是这种升降熨烫台的平面示意图． $\mathit{AB}$和 $\mathit{CD}$是两根相同长度的活动支撑杆，点 $O$是它们的连接点， $\mathit{OA}=\mathit{OC}$， $h\left(\mathit{cm}\right)$表示熨烫台的高度．

（1）如图 $2-1$．若 $\mathit{AB}=\mathit{CD}=110\mathit{cm}$， $\angle \mathit{AOC}=120°$，求 $h$的值；

（2）爱动脑筋的小明发现，当家里这种升降熨烫台的高度为 $120\mathit{cm}$时，两根支撑杆的夹角 $\angle \mathit{AOC}$是 $74°$（如图 $2-2)$．求该熨烫台支撑杆 $\mathit{AB}$的长度（结果精确到 $1\mathit{cm})$．

（参考数据： $\sin 37°\approx 0.6$， $\cos 37°\approx 0.8$， $\sin 53°\approx 0.8$， $\cos 53°\approx 0.6)$

小丽用两锐角分别为和的三角尺测量一棵树的高度．如图，已知，，，那么这棵树大约有多高？（结果精确到，

如图1为放置在水平桌面上的台灯，底座的高为，长度均为的连杆，与始终在同一平面上．

（1）转动连杆，，使成平角，，如图2，求连杆端点离桌面的高度．

（2）将（1）中的连杆再绕点逆时针旋转，使，如图3，问此时连杆端点离桌面的高度是增加还是减少？增加或减少了多少？（精确到，参考数据：，

图1是一辆在平地上滑行的滑板车，图2是其示意图．已知车杆长，车杆与脚踏板所成的角，前后轮子的半径均为，求把手离地面的高度（结果保留小数点后一位；参考数据：，，．

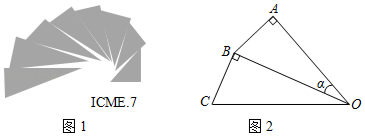
图1是第七届国际数学教育大会 $\left(\mathit{ICME}\right)$ 会徽，在其主体图案中选择两个相邻的直角三角形，恰好能组合得到如图2所示的四边形 $\mathit{OABC}$ ．若 $\mathit{AB}=\mathit{BC}=1$ ， $\angle \mathit{AOB}=\alpha$ ，则 $O{C}^2$ 的值为 $($ 　　 $)$

A．

$\frac{1}{{\sin }^2\alpha }+1$

B．

${\sin }^2\alpha +1$

C．

$\frac{1}{{\cos }^2\alpha }+1$

D．

${\cos }^2\alpha +1$

图①、图②分别是某种型号跑步机的实物图与示意图．已知跑步机手柄 AB与地面 DE平行，踏板 CD长为1.5 m， CD与地面 DE的夹角 $\angle \mathit{CDE}＝15°$ ，支架 AC长为1 m， $\angle \mathit{ACD}＝75°$ ，求跑步机手柄 AB所在直线与地面 DE之间的距离．（结果精确到0.1 m．参考数据： $\mathit{sin}15°\approx 0.26$ ， $\mathit{cos}15°\approx 0.97$ ， $\mathit{tan}15°\approx 0.27$ ， $\sqrt{3}\approx 1.73$ ）

某工程队准备从 $A$到 $B$修建一条隧道，测量员在直线 $\mathit{AB}$的同一侧选定 $C$， $D$两个观测点，如图．测得 $\mathit{AC}$长为 $\frac{3\sqrt{2}}{2}\mathit{km}$， $\mathit{CD}$长为 $\frac{3}{4}(\sqrt{2}+\sqrt{6})\mathit{km}$， $\mathit{BD}$长为 $\frac{3}{2}\mathit{km}$， $\angle \mathit{ACD}=60°$， $\angle \mathit{CDB}=135°(A$、 $B$、 $C$、 $D$在同一水平面内）．

（1）求 $A$、 $D$两点之间的距离；

（2）求隧道 $\mathit{AB}$的长度．

为进一步加强疫情防控工作，避免在测温过程中出现人员聚集现象，某学校决定安装，该设备通过探测人体红外辐射能量对进入测温区域的人员进行快速测温，无需人员停留和接触，安装说明书的部分内容如表．

名称	红外线体温检测仪
安装示意图
技术参数	探测最大角： $\angle \mathit{OBC}＝73.14°$
	探测最小角： $\angle \mathit{OAC}＝30.97°$
安装要求	本设备需安装在垂直于水平地面AC的支架CP上

根据以上内容，解决问题：

学校要求测温区域的宽度AB为4m，请你帮助学校确定该设备的安装高度OC．

（结果精确到0.1m，参考数据： $\mathit{sin}73.14°\approx 0.957，\mathit{cos}73.14°\approx 0.290$，t $\mathit{an}73.14°\approx 3.300$， $\mathit{sin}30.97°\approx 0.515$， $\mathit{cos}30.97°\approx 0.857$， $\text{t}\mathit{an}30.97°\approx 0.600$）

随州市新水一桥（如图1）设计灵感来源于市花 $--$兰花，采用蝴蝶兰斜拉桥方案，设计长度为258米，宽32米，为双向六车道，2018年4月3日通车．斜拉桥又称斜张桥，主要由索塔、主梁、斜拉索组成．某座斜拉桥的部分截面图如图2所示，索塔 $\mathit{AB}$和斜拉索（图中只画出最短的斜拉索 $\mathit{DE}$和最长的斜拉索 $\mathit{AC}$）均在同一水平面内， $\mathit{BC}$在水平桥面上．已知 $\angle \mathit{ABC}=\angle \mathit{DEB}=45°$， $\angle \mathit{ACB}=30°$， $\mathit{BE}=6$米， $\mathit{AB}=5\mathit{BD}$．

（1）求最短的斜拉索 $\mathit{DE}$的长；

（2）求最长的斜拉索 $\mathit{AC}$的长．

图1是安装在倾斜屋顶上的热水器，图2是安装热水器的侧面示意图．已知屋面 AE的倾斜角∠ EAD为22°，长为2米的真空管 AB与水平线 AD的夹角为37°，安装热水器的铁架竖直管 CE的长度为0.5米．

（1）真空管上端 B到水平线 AD的距离．

（2）求安装热水器的铁架水平横管 BC的长度（结果精确到0.1米）．

（参考数据： $\sin {37}^{\circ }\approx \frac{3}{5}$ ， $\cos {37}^{\circ }\approx \frac{4}{5}$ ， $\tan {37}^{\circ }\approx \frac{3}{4}$ ， $\sin {22}^{\circ }\approx \frac{3}{8}$ ， $\cos {22}^{\circ }\approx \frac{15}{16}$ ， $\tan {22}^{\circ }\approx \frac{2}{5}$ ）