初中数学解直角三角形的应用试题

拓展小组研制的智能操作机器人，如图1，水平操作台为 $l$ ，底座 $\mathit{AB}$ 固定，高 $\mathit{AB}$ 为 $50\mathit{cm}$ ，连杆 $\mathit{BC}$ 长度为 $70\mathit{cm}$ ，手臂 $\mathit{CD}$ 长度为 $60\mathit{cm}$ ．点 $B$ ， $C$ 是转动点，且 $\mathit{AB}$ ， $\mathit{BC}$ 与 $\mathit{CD}$ 始终在同一平面内．

（1）转动连杆 $\mathit{BC}$ ，手臂 $\mathit{CD}$ ，使 $\angle \mathit{ABC}=143°$ ， $\mathit{CD}//l$ ，如图2，求手臂端点 $D$ 离操作台 $l$ 的高度 $\mathit{DE}$ 的长（精确到 $1\mathit{cm}$ ，参考数据： $\sin 53°\approx 0.8$ ， $\cos 53°\approx 0.6)$ ．

（2）物品在操作台 $l$ 上，距离底座 $A$ 端 $110\mathit{cm}$ 的点 $M$ 处，转动连杆 $\mathit{BC}$ ，手臂 $\mathit{CD}$ ，手臂端点 $D$ 能否碰到点 $M$ ？请说明理由．

如图为放置在水平桌面上的台灯的平面示意图，灯臂AO长为40cm，与水平面所形成的夹角∠OAM为75°．由光源O射出的边缘光线OC，OB与水平面所形成的夹角∠OCA，∠OBA分别为90°和30°，求该台灯照亮水平面的宽度BC（不考虑其他因素，结果精确到0.1cm．温馨提示： $\mathit{sin}75°\approx 0.97，$ $\mathit{cos}75°\approx 0.26，\sqrt{3}\approx 1.73$．

保护视力要求人写字时眼睛和笔端的距离应超过 $30\mathit{cm}$，图1是一位同学的坐姿，把他的眼睛 $B$，肘关节 $C$和笔端 $A$的位置关系抽象成图2的 $\mathit{\Delta ABC}$，已知 $\mathit{BC}=30\mathit{cm}$， $\mathit{AC}=22\mathit{cm}$， $\angle \mathit{ACB}=53°$，他的这种坐姿符合保护视力的要求吗？请说明理由．（参考数据： $\sin 53°\approx 0.8$， $\cos 53°\approx 0.6$， $\tan 53°\approx 1.3)$

如图，已知在Rt△ABC中， $\angle \mathit{ABC}＝90°$，点D沿BC自B向C运动（点D与点B、C不重合），作 $\mathit{BE}\perp \mathit{AD}$于E， $\mathit{CF}\perp \mathit{AD}$于F，则BE+CF的值（　　）

A．不变B．增大

C．减小D．先变大再变小

“兰州中山桥“位于兰州滨河路中段白塔山下、金城关前，是黄河上第一座真正意义上的桥梁，有“天下黄河第一桥“之美誉．它像一部史诗，记载着兰州古往今来历史的变迁．桥上飞架了5座等高的弧形钢架拱桥．

小芸和小刚分别在桥面上的A，B两处，准备测量其中一座弧形钢架拱梁顶部C处到桥面的距离．已知AB＝20m，小芸在A处测得∠CAB＝36°，小刚在B处测得∠CBA＝43°，求弧形钢架拱梁顶部C处到桥面的距离．（结果精确到0.1m）（参考数据sin36°≈0.59，cos36°≈0.81，tan36°≈0.73，sin43°≈0.68，cos43°≈0.73，tan43°≈0.93）

太阳能光伏建筑是现代绿色环保建筑之一，老张准备把自家屋顶改建成光伏瓦面，改建前屋顶截面 $\mathit{\Delta ABC}$如图2所示， $\mathit{BC}=10$米， $\angle \mathit{ABC}=\angle \mathit{ACB}=36°$，改建后顶点 $D$在 $\mathit{BA}$的延长线上，且 $\angle \mathit{BDC}=90°$，求改建后南屋面边沿增加部分 $\mathit{AD}$的长．（结果精确到0.1米）

（参考数据： $\sin 18°\approx 0.31$， $\cos 18°\approx 0.95$． $\tan 18°\approx 0.32$， $\sin 36°\approx 0.59$． $\cos 36°\approx 0.81$， $\tan 36°\approx 0.73)$

某工程队准备从 $A$ 到 $B$ 修建一条隧道，测量员在直线 $\mathit{AB}$ 的同一侧选定 $C$ ， $D$ 两个观测点，如图．测得 $\mathit{AC}$ 长为 $\frac{3\sqrt{2}}{2}\mathit{km}$ ， $\mathit{CD}$ 长为 $\frac{3}{4}(\sqrt{2}+\sqrt{6})\mathit{km}$ ， $\mathit{BD}$ 长为 $\frac{3}{2}\mathit{km}$ ， $\angle \mathit{ACD}=60°$ ， $\angle \mathit{CDB}=135°(A$ 、 $B$ 、 $C$ 、 $D$ 在同一水平面内）．

（1）求 $A$ 、 $D$ 两点之间的距离；

（2）求隧道 $\mathit{AB}$ 的长度．

汽车超速行驶是交通安全的重大隐患，为了有效降低交通事故的发生，许多道路在事故易发路段设置了区间测速．如图，学校附近有一条笔直的公路 $l$，其间设有区间测速，所有车辆限速40千米 $/$小时．数学实践活动小组设计了如下活动：在 $l$上确定 $A$， $B$两点，并在 $\mathit{AB}$路段进行区间测速．在 $l$外取一点 $P$，作 $\mathit{PC}\perp l$，垂足为点 $C$．测得 $\mathit{PC}=30$米， $\angle \mathit{APC}=71°$， $\angle \mathit{BPC}=35°$．上午9时测得一汽车从点 $A$到点 $B$用时6秒，请你用所学的数学知识说明该车是否超速．（参考数据： $\sin 35°\approx 0.57$， $\cos 35°\approx 0.82$， $\tan 35°\approx 0.70$， $\sin 71°\approx 0.95$， $\cos 71°\approx 0.33$， $\tan 71°\approx 2.90)$

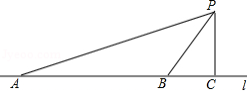
如图1，在△ ABC中，设∠ A、∠ B、∠ C的对边分别为 a， b， c，过点 A作 AD⊥ BC，垂足为 D，会有sin∠ C＝ $\frac{\mathit{AD}}{\mathit{AC}}$ ，则

S _{△ ABC}＝ $\frac{1}{2}$ BC× AD＝ $\frac{1}{2}$ × BC× ACsin∠ C＝ $\frac{1}{2}$ absin∠ C，

即 S _{△ ABC}＝ $\frac{1}{2}$ absin∠ C

同理 S _{△ ABC}＝ $\frac{1}{2}$ bcsin∠ A

S _{△ ABC}＝ $\frac{1}{2}$ acsin∠ B

通过推理还可以得到另一个表达三角形边角关系的定理﹣余弦定理：

如图2，在△ ABC中，若∠ A、∠ B、∠ C的对边分别为 a， b， c，则

a ²＝ b ²+ c ²﹣2 bccos∠ A

b ²＝ a ²+ c ²﹣2 accos∠ B

c ²＝ a ²+ b ²﹣2 abcos∠ C

用上面的三角形面积公式和余弦定理解决问题：

（1）如图3，在△ DEF中，∠ F＝60°，∠ D、∠ E的对边分别是3和8．求 S _{△ DEF}和 DE ²．

解： S _{△ DEF}＝ EF× DFsin∠ F＝ 　　；

DE ²＝ EF ²+ DF ²﹣2 EF× DFcos∠ F＝ 　　．

（2）如图4，在△ ABC中，已知 AC＞ BC，∠ C＝60°，△ ABC'、△ BCA'、△ ACB'分别是以 AB、 BC、 AC为边长的等边三角形，设△ ABC、△ ABC'、△ BCA'、△ ACB'的面积分别为 S ₁、 S ₂、 S ₃、 S ₄，求证： S ₁+ S ₂＝ S ₃+ S ₄．

如图，地面上小山的两侧有 A， B两地，为了测量 A， B两地的距离，让一热气球从小山西侧 A地出发沿与 AB成30°角的方向，以每分钟40 m的速度直线飞行，10分钟后到达 C处，此时热气球上的人测得 CB与 AB成70°角，请你用测得的数据求 A， B两地的距离 AB长．（结果用含非特殊角的三角函数和根式表示即可）

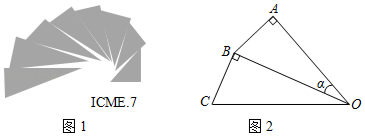
图1是第七届国际数学教育大会 $\left(\mathit{ICME}\right)$ 会徽，在其主体图案中选择两个相邻的直角三角形，恰好能组合得到如图2所示的四边形 $\mathit{OABC}$ ．若 $\mathit{AB}=\mathit{BC}=1$ ， $\angle \mathit{AOB}=\alpha$ ，则 $O{C}^2$ 的值为 $($ 　　 $)$

A．

$\frac{1}{{\sin }^2\alpha }+1$

B．

${\sin }^2\alpha +1$

C．

$\frac{1}{{\cos }^2\alpha }+1$

D．

${\cos }^2\alpha +1$

图①、图②分别是某种型号跑步机的实物图与示意图．已知跑步机手柄 AB与地面 DE平行，踏板 CD长为1.5 m， CD与地面 DE的夹角 $\angle \mathit{CDE}＝15°$ ，支架 AC长为1 m， $\angle \mathit{ACD}＝75°$ ，求跑步机手柄 AB所在直线与地面 DE之间的距离．（结果精确到0.1 m．参考数据： $\mathit{sin}15°\approx 0.26$ ， $\mathit{cos}15°\approx 0.97$ ， $\mathit{tan}15°\approx 0.27$ ， $\sqrt{3}\approx 1.73$ ）

某工程队准备从 $A$到 $B$修建一条隧道，测量员在直线 $\mathit{AB}$的同一侧选定 $C$， $D$两个观测点，如图．测得 $\mathit{AC}$长为 $\frac{3\sqrt{2}}{2}\mathit{km}$， $\mathit{CD}$长为 $\frac{3}{4}(\sqrt{2}+\sqrt{6})\mathit{km}$， $\mathit{BD}$长为 $\frac{3}{2}\mathit{km}$， $\angle \mathit{ACD}=60°$， $\angle \mathit{CDB}=135°(A$、 $B$、 $C$、 $D$在同一水平面内）．

（1）求 $A$、 $D$两点之间的距离；

（2）求隧道 $\mathit{AB}$的长度．

为进一步加强疫情防控工作，避免在测温过程中出现人员聚集现象，某学校决定安装，该设备通过探测人体红外辐射能量对进入测温区域的人员进行快速测温，无需人员停留和接触，安装说明书的部分内容如表．

名称	红外线体温检测仪
安装示意图
技术参数	探测最大角： $\angle \mathit{OBC}＝73.14°$
	探测最小角： $\angle \mathit{OAC}＝30.97°$
安装要求	本设备需安装在垂直于水平地面AC的支架CP上

根据以上内容，解决问题：

学校要求测温区域的宽度AB为4m，请你帮助学校确定该设备的安装高度OC．

（结果精确到0.1m，参考数据： $\mathit{sin}73.14°\approx 0.957，\mathit{cos}73.14°\approx 0.290$，t $\mathit{an}73.14°\approx 3.300$， $\mathit{sin}30.97°\approx 0.515$， $\mathit{cos}30.97°\approx 0.857$， $\text{t}\mathit{an}30.97°\approx 0.600$）

随州市新水一桥（如图1）设计灵感来源于市花 $--$兰花，采用蝴蝶兰斜拉桥方案，设计长度为258米，宽32米，为双向六车道，2018年4月3日通车．斜拉桥又称斜张桥，主要由索塔、主梁、斜拉索组成．某座斜拉桥的部分截面图如图2所示，索塔 $\mathit{AB}$和斜拉索（图中只画出最短的斜拉索 $\mathit{DE}$和最长的斜拉索 $\mathit{AC}$）均在同一水平面内， $\mathit{BC}$在水平桥面上．已知 $\angle \mathit{ABC}=\angle \mathit{DEB}=45°$， $\angle \mathit{ACB}=30°$， $\mathit{BE}=6$米， $\mathit{AB}=5\mathit{BD}$．

（1）求最短的斜拉索 $\mathit{DE}$的长；

（2）求最长的斜拉索 $\mathit{AC}$的长．