某商场为了吸引顾客，设计了一个摸球获奖的箱子，箱子中共有20个球，其中红球2个，兰球3个，黄球5个，白球10个，并规定购买100元的商品，就有一次摸球的机会，摸到红、兰、黄、白球的(一次只能摸一个)，顾客就可以分别得到80元、30元、10元、0元购物卷，凭购物卷仍然可以在商场购买，如果顾客不愿意摸球，那么可以直接获得购物卷10元.
(1)每摸一次球所获购物卷金额的平均值是多少？
(2)你若在此商场购买100元的货物，两种方式中你应选择哪种方式？为什么？
某中学七年级有8个班，要从中选出2个班代表学校参加某项活动。七（1）班必须参加，另外再从七（2）至七（8）班选出1个班．七（5）班有学生建议用如下的方法：从装有四个标有数字1、2、3、4的球袋中摸出1个球，记下数字，放回摇匀后再摸出1个球（球的大小、形状与质量完全一样），两次摸出的球上的数字和是几，就选几班。（1）分别求出选七（2）、七（5）、七（8）班的概率；（2）你认为这种方法公平吗？如不公平，请你设计一个公平的方案
小王和小明用如图所示的同一个转盘进行“配紫色”游戏，游戏规则如下：连续转动两次转盘，如果两次转出的颜色相同或配成紫色（若其中一次转盘转出蓝色，另一次转出红色，则配成紫色）则小王得1分，否则小明得1分（如果指针恰好指在分割线上，那么重转一次，直到指针指向一种颜色为止）。
（1）请你通过列表法分别求出小王和小明获胜的概率。
（2）你认为这个游戏对双方公平吗？请说明理由：若不公平，请修改规则，使游戏对双方公平。
小明手中有4张背面相同的扑克牌：红桃A、红桃2、黑桃A、黑桃2。先将4张牌背面朝上洗匀，再让小刚抽牌。
（1）小刚从中任意抽取一张扑克牌，抽到红桃的概率为 。
（2）小刚从中任意抽取两张扑克牌。游戏规则规定：小刚抽到的两张牌是一红、一黑，则小刚胜，否则小明胜，问该游戏对双方是否公平。（利用树状图或列表说明）
某电脑公司现有A，B，C三种型号的甲品牌电脑和D，E两种型号的乙品牌电脑。希望中学要从甲、乙两种品牌电脑中各选购一种型号的电脑。
(1) 写出所有选购方案(利用树状图或列表方法表示）；
(2) 如果(1)中各种选购方案被选中的可能性相同，那么B型号电脑被选中的概率是多少？
一个袋中有3张形状大小完全相同的卡片，编号为1,2,3，先任取一张，将其编号记为m，再从剩下的两张中任取一张，将其编号记为n.
（1）请用树状图或者列表法，表示事件发生的所有可能情况；
（2）求关于x的方程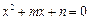
有两个不相等实数根的概率.
某射击运动员在相同条件下的射击160次，其成绩记录如下：
| 射击次数 |
20 |
40 |
60 |
80 |
100 |
120 |
140 |
160 |
| 射中9环以上的次数 |
15 |
33 |
|
63 |
78 |
97 |
111 |
127 |
| 射中9环以上的频率 |
0.75 |
0.83 |
0.80 |
0.79 |
0.79 |
|
0.79 |
0.81 |
（1）根据上表中的信息将两个空格的数据补全（射中9环以上的次数为整数，频率精确到0.01）；
（2）根据频率的稳定性，估计这名运动员射击一次时“射中9环以上”的概率（精确到0.1），并简述理由.
甲口袋中装有2个小球，它们分别标有数字1、2，乙口袋中装有3个小球，它们分别标有数字3、4、5．现分别从甲、乙两个口袋中随机地各取出1个小球，请你用列举法（画树状图或列表的方法）求取出的两个小球上的数字之和为5的概率.
．小红和小慧玩纸牌游戏．如图是同一副扑克中的4张牌的正面，将它们正面朝下洗匀后放在桌上，小红先从中抽出一张，小慧从剩余的3张牌中也抽出一张． 
（1）请用树状图表示出两人抽牌可能出现的所有结果；
（2）求抽出的两张牌都是偶数的概率．
正四面体各面分别标有数字1、2、3、4，正六面体各面分别标有数字1、2、3、4、5、6，同时掷这两个正多面体，并将它们朝下面上的数字相加．
（1）请用树状图或列表的方法表示可能出现的所有结果；
（2）求两个正多面体朝下面上的数字之和是3的倍数的概率．
在一个口袋中有3个完全相同的小球，把它们分别标号为1、2、3，随机地摸取一个小球后放回，再随机地摸出一个小球．求“两次取的小球的标号相同”的概率。请借助列表法或树形图说明理由。
某中学共有学生2000名，各年级男女生人数如下表：
| |
六年级 |
七年级 |
八年级 |
九年级 |
| 男生 |
250 |
z |
254 |
258 |
| 女生 |
x |
244 |
y |
252 |
若从全校学生中任意抽一名，抽到六年级女生的概率是0.12；若将各年级的男、女生人数制作成扇形统计图，八年级女生对应扇形的圆心角为44.28°．
（1）求x，y，z的值；
（2）求各年级男生的中位数；
（3）求各年级女生的平均数；
（4）从八年级随机抽取36名学生参加社会实践活动，求抽到八年级某同学的概率．
下图是由转盘和指针组成的装置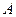
、
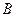，两个转盘分别被分成三个面积相等的扇形. 装置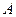上的数字分别是1，6，8，装置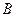上的数字分别是4，5，7. 这两个装置除了表面数字不同外，其他构造完全相同. 现在你和另外一个同学分别同时用力转动装置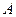、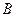中的指针，如果我们规定指针停留在较大数字的一方获胜（若指针恰好停留在分界线上，则重新转动
一次，直到指针停留在某一数字为止），那么你选择的装置是 ，请说明理由．
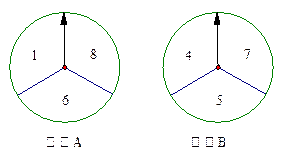
如图3，甲转盘被分成3个面积相等的扇形，乙转盘被分成2个面积相等的扇形．随机地转动指针(当指针指在边界线上时视为无效，重转)．
请解答下列问题．
⑴ 在图甲中，随机地转动指针，指针指向扇形2的概率是_____________；
⑵ 分别转动图甲和图乙的指针，两个指针停止时所指区域内的数之和为6或7，试用树状图或列表法求出其概率．
试题篮
()
粤公网安备 44130202000953号
指针指向每个区域的可能性相等（不计指针与两个区域交线重合的情形），将所得区域的序号相乘，比较所得积为奇数和偶数的概率的大小。有人说：因为两个转盘中奇数序号比偶数序号多，显然所得积为奇数的概率大，你同意他的说法吗？请说明理由。
